Γλώσσα:
Εμβαδόν ορθογώνιο παραλληλόγραμμο
Εμβαδόν ορθογώνιο παραλληλόγραμμο, τύποι για τον υπολογισμό της περιοχής των ορθογωνίων ανάλογα με τα γνωστά δεδομένα προέλευσης, μια αριθμομηχανή για την εύρεση της περιοχής σε απευθείας σύνδεση και έναν πίνακα περιλήψεων με τους τύπους περιοχής του ορθογωνίου. Η αριθμομηχανή μας θα σας βοηθήσει να υπολογίσετε την περιοχή ενός ορθογωνίου δωρεάν online χρησιμοποιώντας διάφορους τύπους ή να ελέγξετε τους ήδη ολοκληρωμένους υπολογισμούς.
Πίνακας τύπων περιοχής ορθογωνίου (στο τέλος της σελίδας)
1
Εμβαδόν ορθογώνιο παραλληλόγραμμο δύο όψεων
... προετοιμασία ...
a - πλευρά
b - πλευρά
2
Εμβαδόν ορθογώνιο παραλληλόγραμμο της περιμέτρου και μία από τις πλευρές
Στον καθορισμένο τύπο, υπολογίζεται η περίμετρος του ορθογωνίου:
... προετοιμασία ...
a (ή b) - πλευρά
P - περίμετρος
3
Διαγώνια και πλευρική ορθογώνια περιοχή
... προετοιμασία ...
a (ή b) - πλευρά
d - διαγώνιος
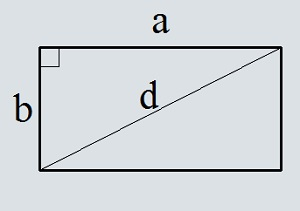
4
Εμβαδόν ορθογώνιο παραλληλόγραμμο των διαγώνιων και η γωνία μεταξύ τους
... προετοιμασία ...
d - διαγώνιος
α° - η γωνία μεταξύ των διαγωνίων του
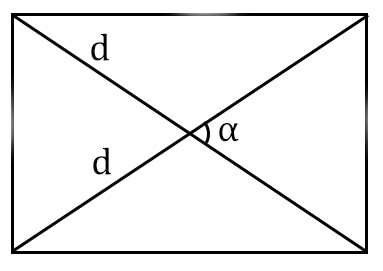
5
Εμβαδόν ορθογώνιο παραλληλόγραμμο της πλευράς και η ακτίνα του περιγεγραμμένου κύκλου
... προετοιμασία ...
a (ή b) - πλευρά
R - ακτίνα περιγράφεται περιφέρειας
6
Εμβαδόν ορθογώνιο παραλληλόγραμμο της πλευράς και η διάμετρος του περιορισμένου κύκλου
... προετοιμασία ...
a (ή b) - πλευρά
D - διάμετρος κύκλου
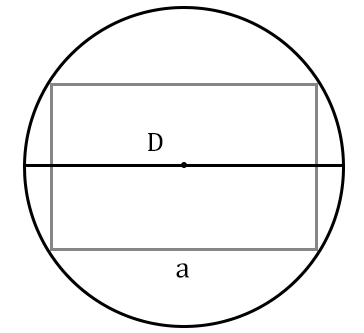
Σημείωση:
Εάν η γωνία προσδιορίζεται στα ακτίνια στα δεδομένα πηγής, τότε για μετατροπή σε μοίρες μπορείτε να χρησιμοποιήσετε τον τύπο: 1 radian × (180/π)° = 57,296°
Πίνακας τύπων περιοχής ορθογωνίου
| τα αρχικά δεδομένα (ενεργό σύνδεσμο για να μεταβείτε στην αριθμομηχανή) |
σκίτσο | ο τύπος | |
| 1 | δύο πλευρές | |
|
| 2 | περίμετρος και μία πλευρά | |
|
| 3 | διαγώνιος και πλευρικός | |
|
| 4 | διαγώνια και γωνία μεταξύ τους | |
|
| 5 |
πλευρά και ακτίνα του περιορισμένου κύκλου |
|
|
| 6 | πλευρά και διάμετρος του περιορισμένου κύκλου | |