Jazyk:
Obsah obdélníku
Obsah obdélníku, vzorce pro výpočet plochy různých typů trojúhelníků v závislosti na známých zdrojových datech, kalkulačka pro nalezení oblasti online a tabulka s vzorci oblastí trojúhelníků. Obsah obdélníku, vzorce pro výpočet čtvercových obdélníkuů v závislosti na známých zdrojových datech, kalkulačka pro nalezení Obsahi online a kontingenční tabulka s vzorci čtverců obdélníku.
Tabulka se vzorci čtvercového obdélníku (na konci stránky)
1
Obsah obdélníku přes dvě strany

... příprava ...
a - strana
b - strana
2
Obsah obdélníku přes obvod a jednu ze stran

V uvedeném vzorci se vypočítá obvodová plocha obdélníku:
... příprava ...
a (nebo b) - strana
P - obvod
3
Plocha obdélníku diagonálně a po stranách
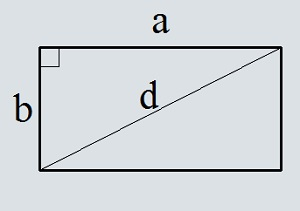
... příprava ...
a (nebo b) - strana
d - úhlopříčka
4
Obsah obdélníku diagonálně a rohu mezi nimi
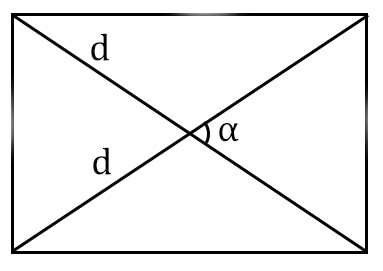
... příprava ...
d - úhlopříčka
α° - úhel mezi диагоналями
5
Obsah obdélníku přes stranu a poloměr popsaného obvodu

... příprava ...
a (nebo b) - strana
R - poloměr popsaného obvodu
6
Obsah obdélníku přes stranu a průměr popsaného obvodu
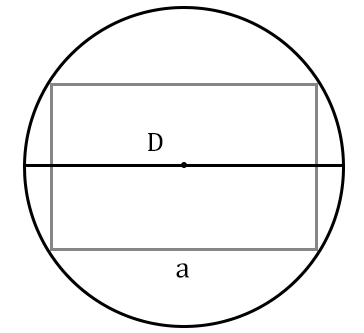
... příprava ...
a (nebo b) - strana
D - průměr popsaného obvodu
Poznámka:
Pokud je úhel v zdrojových datech nastaven na radiány, můžete použít vzorec pro převod do stupňů: 1 radián × (180/π)° = 57,296°
Tabulka se vzorci čtvercového obdélníku
| výchozí data (aktivní odkaz na kalkulačku) |
skica | formule | |
| 1 | dvě strany |  |
|
| 2 | obvod a jedna ze stran |  |
|
| 3 | úhlopříčka a strana |  |
|
| 4 | úhlopříčka a úhel mezi nimi |  |
|
| 5 |
strana a poloměr popsaného obvodu |
 |
|
| 6 | strana a průměr popsaného obvodu |  |