Jazyk:
Velikost čtverce
Velikost čtverce, vzorce, kalkulačka pro výpočet náměstí v režimu on-line. Jsou uvedeny vzorce pro výpočet plochy čtverce při různých vstupních údajů.
Tabulka se vzorci čtvercové oblasti (na konci stránky)
1
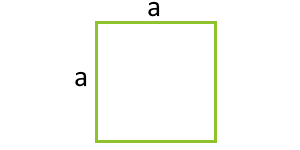
Velikost čtverce přes jeho stranu
... příprava ...
a - strana
2
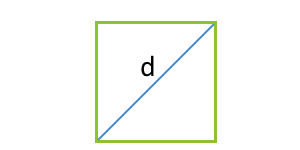
Velikost čtverce přes jeho úhlopříčka
... příprava ...
d - úhlopříčka
3
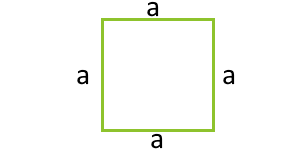
Velikost čtverce, obvod přes
... příprava ...
P - obvod
4
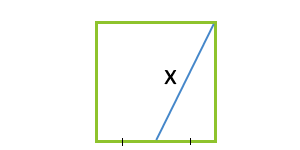
Velikost čtverce přes úsek, provedený z vrcholu čtverce, do středu protější strany
... příprava ...
k - úsek
5
Velikost čtverce přes poloměr vepsané kruhu
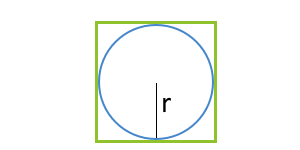
... příprava ...
r - poloměr vepsané kruhu
6
Velikost čtverce přes radius popsaného obvodu
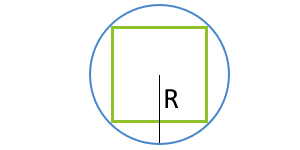
... příprava ...
R - poloměr popsaného obvodu
Poznámka:
Pokud je úhel v zdrojových datech nastaven na radiány, můžete použít vzorec pro převod do stupňů: 1 radián × (180/π)° = 57,296°
Tabulka se vzorci čtvercové oblasti
| výchozí data (aktivní odkaz na kalkulačku) |
skica | formule | |
| 1 | strana |  |
|
| 2 | úhlopříčka |  |
|
| 3 | obvod |  |
|
| 4 | střih k |  |
|
| 5 | poloměr vepsané kruhu |  |
|
| 6 | poloměr popsaného obvodu |  |