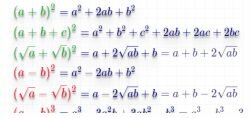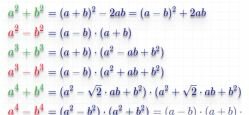Jazyk:
Zkrácené vzorce násobení
Zkrácené vzorce násobení vám umožňují převést matematický výraz na jednodušší formu řešení. Vzorce se používají k otevření stupňovitých závorek, snížení stupně součtu a rozdílu a pro další matematické zjednodušení.
Ve vzorcích níže se místo symbolů «a» a «b» numerické hodnoty, proměnné nebo jakékoliv matematické výrazy a vzorce.