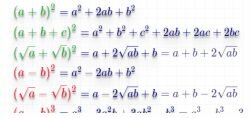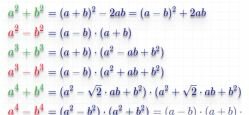Формулы сокращенного умножения
Формулы сокращенного умножения позволяют преобразовать математическое выражение к более простому виду, который позволяет выполнить дальнейшие преобразования или найти нужное решение. Примером формул для математических преобразований является факторизация многочленов, с помощью которой выполнятся понижение степени многочленов. А например с помощью Бинома Ньютона выполняется разложение на отдельные слагаемые степени двух переменных.
Формулы упрощения применяются для раскрытия скобок степеней, понижения степени суммы или разности, а так же для других математических упрощений. В приведенных ниже формулах, вместо символов «a» и «b» могут применяться числовые значения, переменные или любые математические выражения и формулы.
Внизу страницы можно скачать формулы в виде картинок для последующей печати и использования в качестве справочного материала при решении задач.
1. Квадрат суммы
... ... подготовка формул ... ...2. Квадрат разности
3. Сумма и разность квадратов
4. Сумма в третьей степени (куб суммы)
5. Разность в третьей степени (куб разности)
6. Сумма и разность кубов
7. Формулы сокращенного умножения для четвертой степени
8. Формулы сокращенного умножения для пятой степени
9. Формулы сокращенного умножения для шестой степени
10. Формулы сокращенного умножения для степени n, где n - любое натуральное число
11. Формулы сокращенного умножения для степени n, где n - четное положительное число
12. Формулы сокращенного умножения для степени n, где n - нечетное положительное число
13. Некоторые свойства формул
Скачать формулы в виде изображения в виде картинок
Скачать формулы в виде изображения:
