Решение систем линейных уравнений онлайн
Решение систем линейных уравнений онлайн – это нахождение неизвестных переменных входящих в уравнения, при подстановке которых система обращается в равенство.
Решить систему линейных уравнений можно различными способами, например используя метод Крамера и метод Гаусса, метод Жордана Гаусса и метод Кронекера Капелли, или другими способами. Используя наш сервис, вы можете бесплатно в режиме онлайн получить решения разными способами с пошаговыми действиями и пояснениями. Наш калькулятор будет также полезен, если вам необходимо проверить выполненные самостоятельно вычисления.
Решение:
Наш онлайн сервис позволяет решать системы линейных алгебраических уравнений различными способами:
- методом Крамера (правило Крамера)
- методом обратной матрицы
- методом Гаусса-Монтанте (алгоритм Барейса)
- методом Гаусса (метод последовательного исключения переменных)
- методом Гаусса-Жордана (метод полного исключения неизвестных)
При этом сервис предоставляет последовательность решения, а не только ответ.
Дополнительно вы сможете проверить систему уравнений на совместимость.
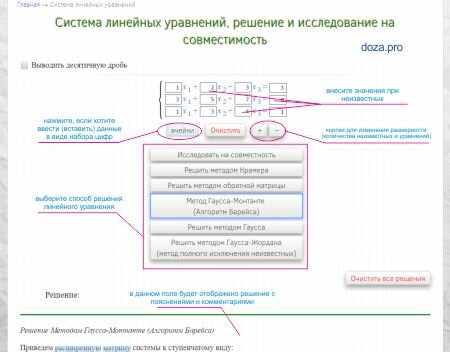
- С помощью знаков «+» и «-» задайте необходимое количество переменных в уравнении. Если в ваше уравнение не входят какие-либо неизвестные, то просто оставьте поля пустыми (незаполненными).
- В ячейках укажите коэффициенты (значения) при неизвестных. Если в исходных данных указано значение x1, x2 и так далее, то в ячейке перед указанными неизвестными укажите значение «1».
- Значения при неизвестных могут быть:
- целые числа:
7,-3,0 - десятичные (конечные и периодические) дроби:
7/8,6.13,-1.3(56),1.2e-4 - арифметические выражения:
1/2+3*(6-4),(6-y)/x^3,2^0.5
- целые числа:
- Далее нажмите на кнопку с названием нужной математической операции.
- Значения в результатах решения можно с помощью мышки перетаскивать на поле исходных данных.
Система линейных алгебраических уравнений (теория)