Площадь трапеции
Площадь трапеции, формулы и калькулятор для вычисления площади в режиме онлайн и сводная таблица с формулами площади трапеции. Приведены формулы для всех типов трапеций и частные случаи для равнобедренных трапеций.
Таблица с формулами площади трапеции (в конце страницы)
Площадь для всех видов трапеции
1
Площадь трапеции по высоте и двум основаниям

2
Площадь трапеции по высоте и средней линии
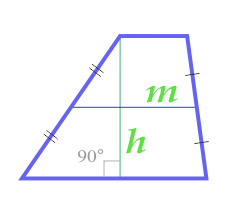
3
Площадь трапеции по четырем сторонам

4
Площадь трапеции по диагонали и углу между диагоналями
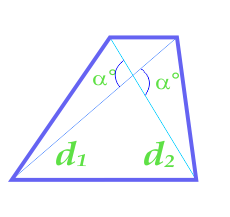
5
Площадь трапеции через ее основания и углы при основании

Площадь равнобедренной трапеции
6
Площадь равнобедренной трапеции через ее стороны

7
Площадь равнобедренной трапеции через малое основание, боковую сторону и угол при большем основании

8
Площадь равнобедренной трапеции через большее основание, боковую сторону и угол при большем основании

9
Площадь равнобедренной трапеции через основания и угол при основании

10
Площадь равнобедренной трапеции через диагонали и угол между диагоналями

11
Площадь равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
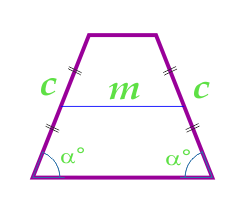
12
Площадь равнобедренной трапеции по радиусу вписанной окружности и углу между сторонами

Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.
13
Площадь равнобедренной трапеции через два ее основания и радиус вписанной окружности
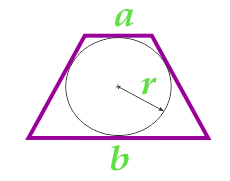
Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.
14
Площадь равнобедренной трапеции через ее основания и угол при большем основании

Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.
15
Площадь равнобедренной трапеции через стороны

Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.
16
Площадь равнобедренной трапеции через основания и среднюю линию
Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.
Примечание:
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади трапеции
В зависимости от известных исходных данных и вида трапеции, площадь трапеции можно вычислить по различным формулам.
| исходные данные (активная ссылка для перехода к калькулятору) |
эскиз | формула | |
| Площадь для всех видов трапеции | |||
| 1 | высота и два основания |  |
|
| 2 | высота и средняя линия |  |
|
| 3 | четыре стороны |  |
|
| 4 | диагонали и угол между ними |  |
|
| 5 | основания и углы при одном из оснований |  |
|
| Площадь равнобедренной трапеции | |||
| 6 | стороны |  |
|
| 7 | основание, боковые стороны и угол при основании |  |
|
| 8 | основание, боковые стороны и угол при основании |  |
|
| 9 | основания и углы при одном из оснований |  |
|
| 10 | диагонали и угол между ними |  |
|
| 11 | средняя линия, боковые стороны и углы между основанием и боковыми сторонами |  |
|
| 12 | радиус вписанной окружности и угол при основании |  |
|
| 13 | основания и радиус вписанной окружности |  |
|
| 14 | основания и углы при одном из оснований |  |
|
| 15 | основания и боковые стороны |  |
|
| 16 | основания и средняя линия |  |
|
Определения
Площадь трапеции – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой, образованной четырьмя последовательно соединенными отрезками (сторонами), два из которых параллельны друг другу
Трапеция – это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами), два из которых параллельны друг другу.
Основания трапеции – это параллельные стороны трапеции. Трапеция имеет большое и малое основание.
Средняя линия трапеции – это отрезок соединяющий середины боковых сторон трапеции и при этом всегда параллельный основаниям трапеции.
Высота трапеции – это отрезок проведенный между основаниями трапеции под углом 90 градусов к каждому из снований.
Сумма углов трапеции равна 360 градусов.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.