Площадь треугольника
Площадь треугольника, формулы для вычисления площади различных видов треугольников в зависимости от известных исходных данных, калькулятор для нахождения площади онлайн и сводная таблица с формулами площадей треугольников.
Таблица с формулами площади треугольника (в конце страницы)
Скачать формулы площади треугольника в виде картинки или файла PDF (в конце страницы)
Для всех треугольников
1
Площадь треугольника по основанию и высоте
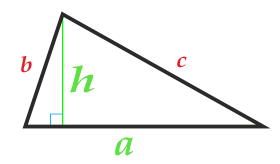
Основанием треугольника может быть выбрана любая из сторон треугольника.
2
Площадь треугольника по двум сторонам и углу между ними
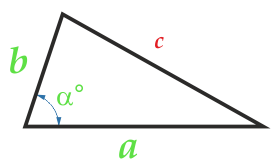
Угол α между сторонами может быть любым: тупым, острым, прямым.
3
Площадь треугольника по радиусу вписанной окружности и трем сторонам
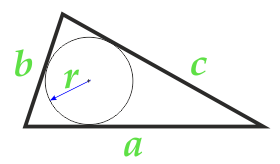
4
Площадь треугольника по радиусу описанной окружности и трем сторонам
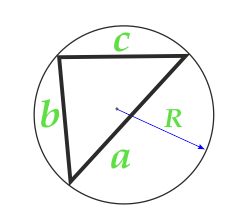
5
Площадь треугольника по формуле Герона
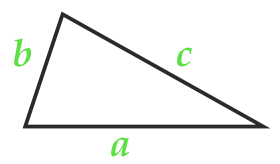
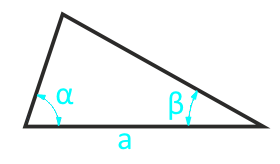
Площадь произвольного треугольника по стороне и двум прилежащим углам
Для равнобедренных треугольников
7
Площадь равнобедренного треугольника по боковым сторонам и основанию
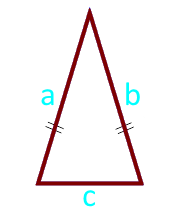
8
Площадь равнобедренного треугольника по боковым сторонам и углу между ними
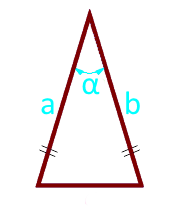
9
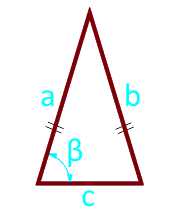
Площадь равнобедренного треугольника по боковой стороне, основанию и углу между ними
10
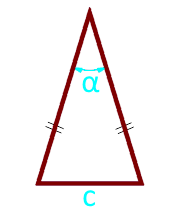
Площадь равнобедренного треугольника по основанию и углу между боковыми сторонами
Для равносторонних треугольников
11
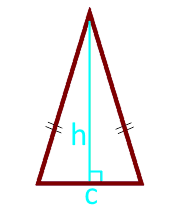
Площадь равнобедренного треугольника по высоте и основанию
12
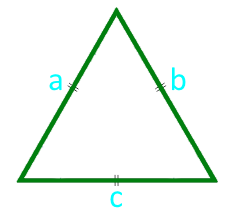
Площадь равностороннего треугольника по стороне
13
Площадь равностороннего треугольника по высоте
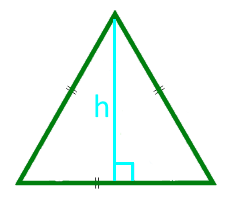
14
Площадь равностороннего треугольника по радиусу вписанной окружности
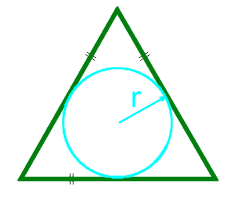
15
Площадь равностороннего треугольника по радиусу описанной окружности
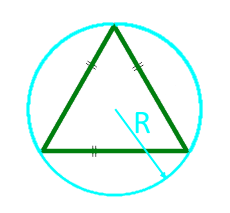
Для прямоугольных треугольников
16
Площадь прямоугольного треугольника по двум катетам
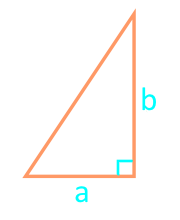
17
Площадь прямоугольного треугольника через гипотенузу и угол
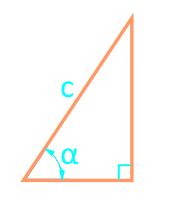
18
Площадь прямоугольного треугольника через катет и угол
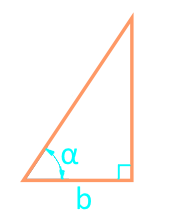
19
Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность
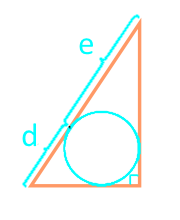
20
Площадь прямоугольного треугольника через гипотенузу и вписанную окружность
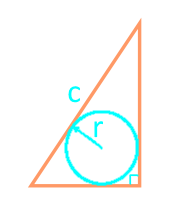
21
Площадь прямоугольного треугольника по формуле Герона
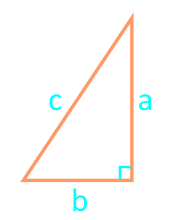
Для вычисления площади треугольника применяются различные формулы, в зависимости от известных исходных данных. Выше приведены формулы и калькулятор, который поможет вычислить площадь треугольника или проверить уже выполненные вычисления. Приведены общие формулы для всех типов треугольников, частные случаи для равносторонних, равнобедренных и прямоугольных треугольников.
Наш калькулятор для вычисления площади поможет вам вычислить площадь разных видов треугольников или проверить уже выполненные вычисления.
В зависимости от вида треугольника и его известных исходных данных, площадь треугольника можно вычислить по различным формулам.
Таблица с формулами площади треугольника
| исходные данные (активная ссылка для перехода к калькулятору) |
эскиз | формула | |
| Для всех треугольников | |||
| 1 | основание и высота |  |
|
| 2 | две стороны и угол между ними |  |
|
| 3 | радиус вписанной окружности и три стороны |  |
|
| 4 | радиус описанной окружности и три стороны |  |
|
| 5 |
три стороны (по формуле Герона) |
 |
где
|
| 6 | сторона и два прилежащих угла |  |
|
| Для равнобедренных треугольников | |||
| 7 | боковые стороны и основание |  |
|
| 8 | боковые стороны и угол между ними |  |
|
| 9 | боковые стороны, основание и угол между боковыми сторонами и основанием |  |
|
| 10 | основание и угол между боковыми сторонами |  |
|
| 11 | высота и основание |  |
|
| Для равносторонних треугольников | |||
| 12 | сторона |  |
|
| 13 | высота |  |
|
| 14 | радиус вписанной окружности |  |
|
| 15 | радиусу описанной окружности |  |
|
| Для прямоугольных треугольников | |||
| 16 | два катета | 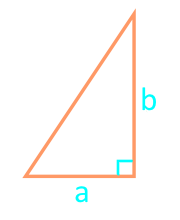 |
|
| 17 | гипотенуза и угол |  |
|
| 18 | катет и угол |  |
|
| 19 | отрезки, на которые делит гипотенузу вписанная окружность | 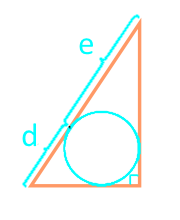 |
|
| 20 | гипотенуза и радиус вписанной окружности |  |
|
| 21 |
три стороны (по формуле Герона) |
 |
где
|
Определения
Площадь треугольника - это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной тремя отрезками (сторонами), которые соединяют три точки (вершины), не лежащие на одной прямой.
Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Отрезки называют сторонами треугольника, а точки – вершинами треугольника.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.





