Ngôn ngữ:
Diện tích tam giác
Diện tích hình tam giác, và các tính Công thức tính diện tích của một trực tuyến. Cung cấp công thức chung cho tất cả các loại hình tam giác, đối với trường hợp cụ thể của giác đều, cân và tam giác vuông góc.
Bảng với công thức diện tích tam giác (ở cuối trang)
Tải xuống các công thức diện tích tam giác dưới dạng hình ảnh hoặc tệp PDF (ở cuối trang)
Đối với tất cả hình tam giác
1
Diện tích của tam giác bởi cơ sở và chiều cao của nó
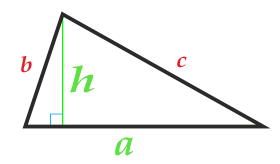
Đảng a
Chiều cao h
Căn cứ của tam giác có thể được chọn từ hai bên của tam giác.
2
Diện tích của tam giác ở hai bên và góc giữa chúng
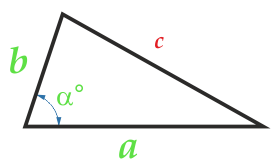
Đảng a
Đảng b
Góc α° giữa các bên a và b
Góc α giữa các cạnh có thể là bất cứ điều gì: thẳng thừng, sắc nét, thẳng.
3
Diện tích của tam giác dọc theo bán kính của vòng tròn ghi và ba bên
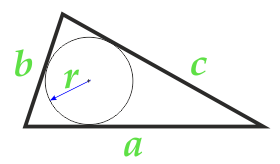
Đảng a
Đảng b
Đảng c
Bán kính r vòng tròn ghi
4
Diện tích của tam giác dọc theo bán kính của đường tròn ngoại tiếp và ba bên
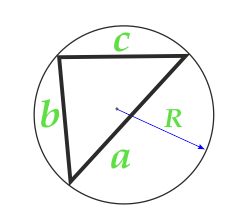
Đảng a
Đảng b
Đảng c
Bán kính R của vòng tròn được bao quanh
5
Diện tích của tam giác theo công thức của Heron
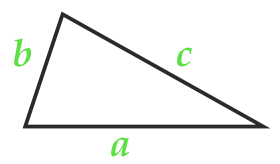
Bán chu vi:
Đảng a
Đảng b
Đảng c
Diện tích của một hình tam giác tùy ý ở bên cạnh và hai góc liền kề
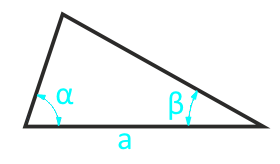
Đảng a
Góc β°
Góc α°
Đối với tam giác cân
7
Diện tích của tam giác cân ở hai bên và gốc
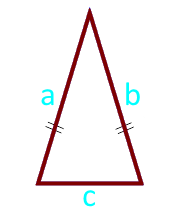
Đảng a (a = b)
Đảng c
8
Diện tích tam giác cân dọc hai bên và góc giữa chúng
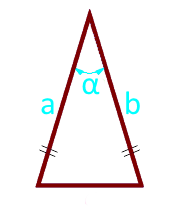
Bên a (a = b)
Góc α° giữa hai bên
9
Diện tích tam giác cân dọc hai bên và góc giữa chúng
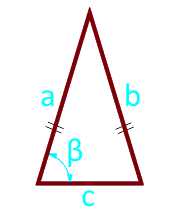
Bên a (a = b)
Các cơ sở của tam giác c
Góc β° giữa cơ sở và bên
10
Diện tích tam giác cân trên cơ sở và góc giữa hai bên
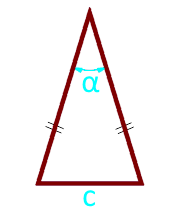
Các cơ sở của tam giác c
Góc α° giữa hai bên
Đối với hình tam giác đều
11
Diện tích của một tam giác cân trong chiều cao và cơ sở
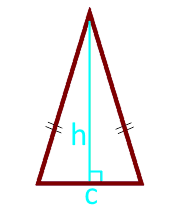
Các cơ sở của tam giác c
Chiều cao h
12
Diện tích của một tam giác đều ở bên cạnh
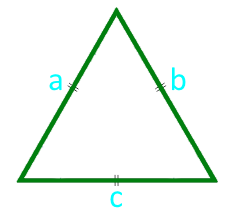
Đảng a (a = b = c)
13
Diện tích của tam giác đều ở chiều cao
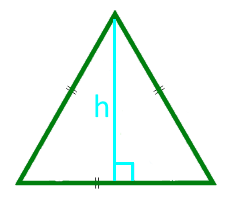
Chiều cao h
14
Diện tích tam giác đều dọc theo bán kính của vòng tròn được ghi
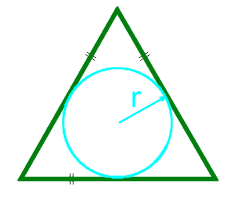
Bán kính r vòng tròn ghi
15
Diện tích tam giác đều dọc theo bán kính của vòng tròn được khoanh vùng
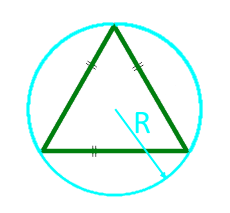
Bán kính R của vòng tròn được bao quanh
Đối với hình tam giác vuông góc bên phải
16
Hình vuông của tam giác vuông có hai chân
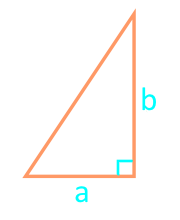
Cathete a
Cathete b
17
Diện tích tam giác vuông qua cạnh huyền và góc
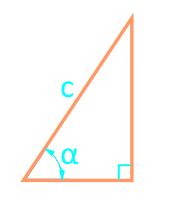
Đảng c
Góc α
18
Diện tích tam giác vuông qua chân và góc
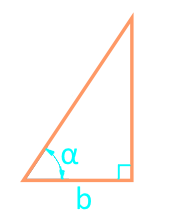
Đảng b
Góc α
19
Diện tích của một tam giác vuông dọc theo phân khúc mà các cạnh huyền chia vòng tròn ghi
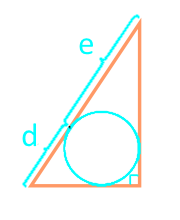
phân khúc d
phân khúc e
20
Diện tích của một tam giác vuông góc qua cạnh huyền và vòng tròn được ghi
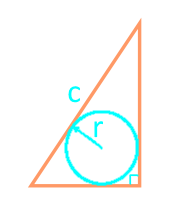
Đảng с
Bán kính r
21
Diện tích của một tam giác vuông bằng cách sử dụng công thức của Heron
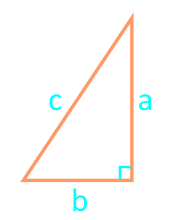
Bán chu vi:
Đảng a
Đảng b
Đảng c
Tùy thuộc vào loại tam giác và dữ liệu nguồn đã biết, diện tích của tam giác có thể được tính bằng các công thức khác nhau.
Bảng với công thức diện tích tam giác
| dữ liệu thô (liên kết hoạt động để đi đến máy tính) |
một bản phác thảo | công thức | |
| Đối với tất cả hình tam giác | |||
| 1 | cơ sở và chiều cao |  |
|
| 2 | hai bên và góc giữa chúng |  |
|
| 3 | bán kính vòng tròn và ba cạnh |  |
|
| 4 | bán kính hình tròn bao quanh và ba cạnh |  |
|
| 5 |
ba mặt (theo công thức Heron sườn) |
 |
ở đâu
|
| 6 | bên và hai góc liền kề |  |
|
| Đối với tam giác cân | |||
| 7 | bên và cơ sở |  |
|
| 8 | các cạnh và góc giữa chúng |  |
|
| 9 | hai bên, cơ sở và góc giữa các bên và cơ sở |  |
|
| 10 | cơ sở và góc giữa các bên |  |
|
| 11 | chiều cao và cơ sở |  |
|
| Đối với hình tam giác đều | |||
| 12 | bên |  |
|
| 13 | chiều cao |  |
|
| 14 | bán kính vòng tròn |  |
|
| 15 | bán kính của vòng tròn đã đăng ký |  |
|
| Đối với hình tam giác vuông góc bên phải | |||
| 16 | hai chân | 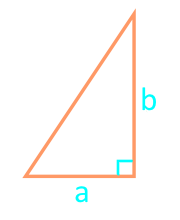 |
|
| 17 | góc cạnh và góc |  |
|
| 18 | chân và góc |  |
|
| 19 | các phân đoạn mà vòng tròn được ghi phân chia cạnh huyền | 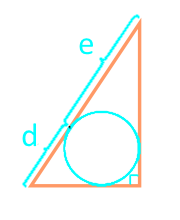 |
|
| 20 | hypotenuse và bán kính vòng tròn ghi |  |
|
| 21 |
ba mặt (theo công thức Heron sườn) |
 |
ở đâu
|





