Flächeninhalt Dreieck
Flächeninhalt Dreieck, Formeln zur Berechnung der Fläche verschiedener dreieckstypen abhängig von den bekannten Quelldaten, Rechner für die Online-Flächensuche und Tabelle mit dreiecksflächenformeln.
Tabelle mit Flächeninhalt Dreieck Formeln (am Ende der Seite)
Laden Sie Dreiecksformeln als Bild oder Datei herunter PDF (am Ende der Seite)
Für alle Dreiecke
1
Flächeninhalt Dreieck an der Basis und Höhe
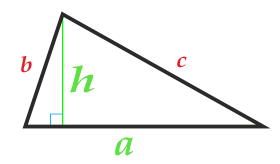
Die Basis des Dreiecks kann auf beiden Seiten des Dreiecks ausgewählt werden.
2
Flächeninhalt Dreieck auf beiden Seiten und der Winkel zwischen Ihnen
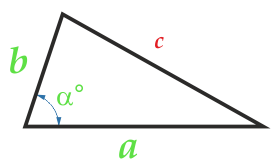
α° – Der Winkel zwischen den Seiten kann beliebig sein: stumpf, scharf, gerade.
3
Flächeninhalt Dreieck entlang des Radius der Beschriftung Kontur und drei Seiten
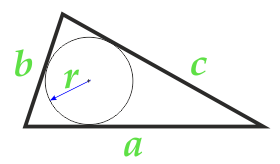
4
Flächeninhalt Dreieck entlang des Radius des umrissenen Kreises und drei Seiten
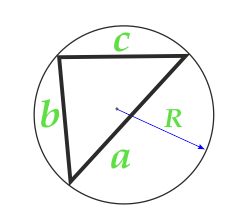
5
Flächeninhalt Dreieck nach der reiherformel
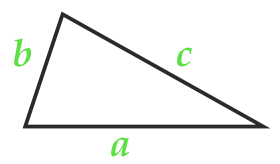
Die Fläche eines beliebigen Dreiecks an der Seite und den beiden angrenzenden Ecken
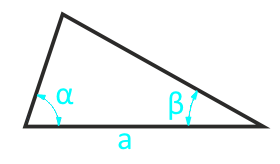
Für gleichschenklige Dreiecke
7
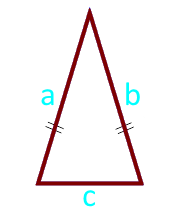
Die Fläche des gleichschenkligen Dreiecks an den Seiten und der Basis
8
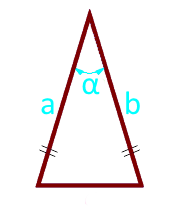
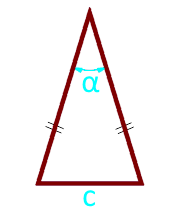
Die Fläche des gleichschenkligen Dreiecks an den Seiten und der Winkel zwischen Ihnen
9
Der Bereich des gleichschenkligen Dreiecks an der Seite, der Basis und des Winkels zwischen Ihnen
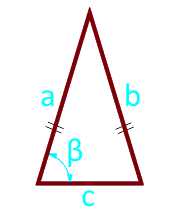
10
Die Fläche des gleichschenkligen Dreiecks an der Basis und der Winkel zwischen den Seiten
Für gleichseitige Dreiecke
11
Die Fläche des gleichschenkligen Dreiecks in Höhe und Basis
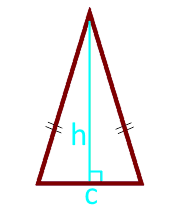
12
Fläche eines gleichseitigen Dreiecks an der Seite
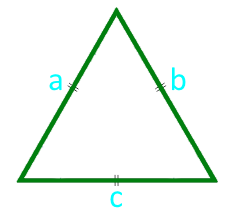
13
Fläche eines gleichseitigen Dreiecks in der Höhe
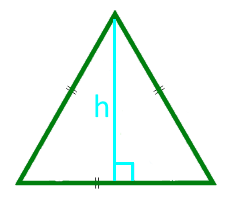
14
Fläche eines gleichseitigen Dreiecks um den Radius der Beschriftung
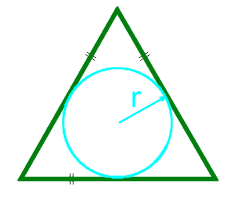
15
Die Fläche eines gleichseitigen Dreiecks entlang des Radius des beschriebenen Kreises
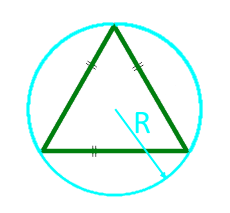
Für rechteckige Dreiecke
16
Bereich eines rechtwinkligen Dreiecks in zwei Beinen
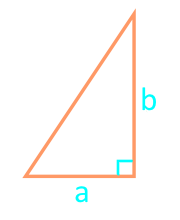
17
Die Fläche eines rechtwinkligen Dreiecks durch die Hypotenuse und den Winkel
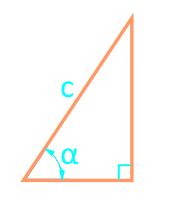
18
Die Fläche eines rechtwinkligen Dreiecks durch den kathet und Winkel
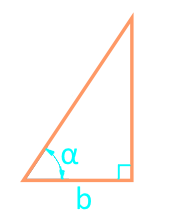
19
Die Fläche eines rechtwinkligen Dreiecks entlang der Segmente, in die der eingeschriebene Kreis die Hypotenuse teilt
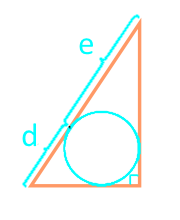
20
Die Fläche eines rechtwinkligen Dreiecks durch die Hypotenuse und den eingeschriebenen Kreis
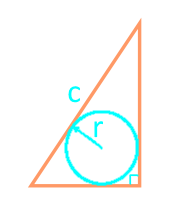
21
Die Fläche eines rechtwinkligen Dreiecks nach der Reiher-Formel
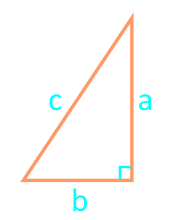
Abhängig von den bekannten Eingaben werden verschiedene Formeln verwendet, um die Fläche eines Dreiecks zu berechnen. Oben finden Sie Formeln und einen Rechner, mit dem Sie die Fläche eines Dreiecks berechnen oder bereits ausgeführte Berechnungen überprüfen können. Allgemeine Formeln werden für alle Arten von Dreiecken gegeben, spezielle Fälle für gleichseitige, gleichschenklige und rechteckige Dreiecke.
Unser quadratrechner hilft Ihnen, die Fläche verschiedener dreieckstypen zu berechnen oder bereits ausgeführte Berechnungen zu überprüfen.
Abhängig von der Art des Dreiecks und seinen bekannten Quelldaten kann die Fläche des Dreiecks anhand verschiedener Formeln berechnet werden.
Tabelle mit Flächeninhalt Dreieck Formeln
| Rohdaten (aktiver Link, um zum Rechner zu gelangen) |
Skizze | Formel | |
| Für alle Dreiecke | |||
| 1 | Basis und Höhe |  |
|
| 2 | zwei Seiten und der Winkel dazwischen |  |
|
| 3 | Radius des eingeschriebenen Kreises und drei Seiten |  |
|
| 4 | der Radius des beschriebenen Kreises und die drei Seiten |  |
|
| 5 |
drei Seiten (nach der Geron-Formel) |
 |
wo
|
| 6 | Seite und zwei benachbarte Ecken |  |
|
| Für gleichschenklige Dreiecke | |||
| 7 | Seiten und Basis |  |
|
| 8 | Seiten und Winkel dazwischen |  |
|
| 9 | Seiten, Basis und Winkel zwischen Seiten und Basis |  |
|
| 10 | Basis und Winkel zwischen den Seiten |  |
|
| 11 | Höhe und Basis |  |
|
| Für gleichseitige Dreiecke | |||
| 12 | Seite |  |
|
| 13 | Höhe |  |
|
| 14 | Radius des eingeschriebenen Kreises |  |
|
| 15 | den Radius des beschriebenen Kreises |  |
|
| Für rechteckige Dreiecke | |||
| 16 | zwei Kathete | 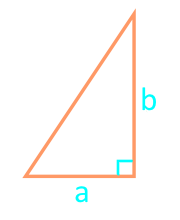 |
|
| 17 | Hypotenuse und Winkel |  |
|
| 18 | kathet und Winkel |  |
|
| 19 | Segmente, in die der eingeschriebene Kreis die Hypotenuse teilt | 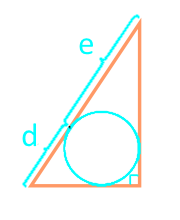 |
|
| 20 | Hypotenuse und Radius des eingeschriebenen Kreises |  |
|
| 21 |
drei Seiten (nach der Geron-Formel) |
 |
wo
|





