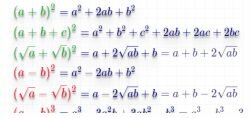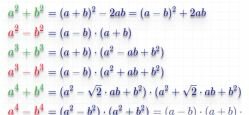Sprache:
Binomische formeln
Binomische formeln - erlaube dir, einen mathematischen ausdruck in ein einfacher zu lösendes denken umzuwandeln. Gekürzte multiplikation formel werden verwendet, um die gradklammern zu öffnen, den grad der summe und der differenz zu verringern und für andere mathematische vereinfachungen.
In den folgenden Formeln statt Zeichen «a» und «b» numerische Werte, Variablen oder mathematische Ausdrücke und Formeln können angewendet werden.