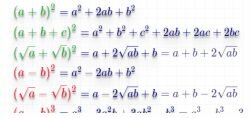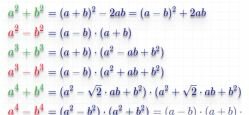Faktorisering
Faktorisering giver dig mulighed for at konvertere et matematisk udtryk til en enklere form, som giver dig mulighed for at udføre yderligere transformationer eller finde den rigtige løsning. Et eksempel på formler til matematiske transformationer er faktorisering af polynomer, ved hjælp af hvilke graden af polynomer reduceres. Og for eksempel udføres ved hjælp af Newtons Binom, nedbrydning i separate vilkår for grad af to variabler.
Forenklingsformler bruges til at eksponere parenteser af grader, reducere graden af en sum eller en forskel og også til andre matematiske forenklinger. I formlerne nedenfor i stedet for tegn «a» og «b» numeriske værdier, variabler eller eventuelle matematiske udtryk og formler kan anvendes.
Nederst på siden kan du downloade formler i form af billeder til efterfølgende udskrivning og bruges som referencemateriale til løsning af problemer.
1. Mængde kvadratisk
... ... udarbejdelse af formler ... ...2. Forskel kvadrat
3. Summen og forskellen på firkanter
4. Beløb i tredje grad
5. Tredje graders forskel
6. Summen og forskellen på terninger
7. Faktorisering for fjerde grad
8. Faktorisering for femte grad
9. Faktorisering for sjette grad
10. Forkortede multiplikationsformler til graden n, hvor n - ethvert naturligt tal
11. Forkortede multiplikationsformler til graden n, hvor n - jævnt positivt antal
12. Forkortede multiplikationsformler til graden n, hvor n - ulige positivt antal
13. Nogle egenskaber ved formler
Download faktorisering som billeder
Download faktorisering
