Areal af en cirkel
Formler og lommeregner til beregning areal af en cirkel for forskellige kildedata. En tabel med formler til areal af en cirkel. Vores lommeregner hjælper dig med at beregne arealet af en cirkel gratis online eller tjekke allerede udførte beregninger.
Tabel med formler for cirkelområdet (i slutningen af siden)
1
Cirkelområde gennem radius
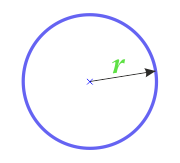
2
Cirkelareal gennem diameter

3
Cirkelområde langs omkredsen

4
Areal af en cirkel gennem en firkant, der er indskrevet i en cirkel

5
Areal af en cirkel, der er indskrevet i en firkant
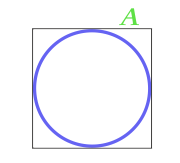
6
Areal af en cirkel beskrevet nær en vilkårlig trekant
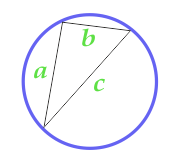
Denne formel er kun anvendelig, hvis en cirkel kan beskrives omkring en trekant, det vil sige, at alle tre hjørner af trekanten skal ligge på en cirkellinie. Trekanten i dette tilfælde kan være en hvilken som helst.
For at beregne arealet af en cirkel beregnes foreløbigt trekantens semiperimeter
7
Området med cirklen beskrevet nær en ligesidet trekant
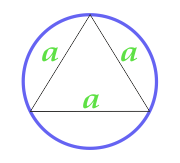
8
Areal af en cirkel beskrevet nær en ligesidet trekant, beregnet af trekantens højde

9
Areal af en cirkel beskrevet i nærheden af en ensartet trekant
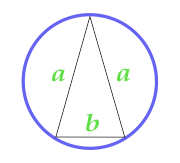
10
Areal af en cirkel beskrevet nær en højre trekant
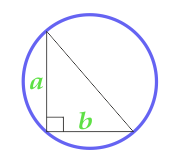
11
Areal af en cirkel, der er indskrevet i en ensartet trekant
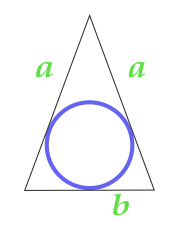
12
Areal af en cirkel, der er indskrevet i en ensartet trekant, beregnet af siderne af trekanten og vinklen mellem dem
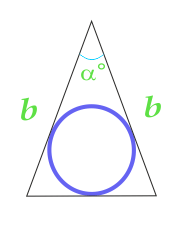
13
Areal af en cirkel indskrevet i en højre trekant
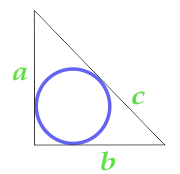
14
Areal af en cirkel, der er indskrevet i en retvinklet trekant, beregnet ved siden og hjørnet
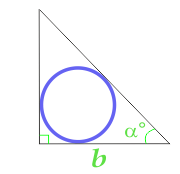
15
Areal af en cirkel, der er indskrevet i en ligesidet trekant
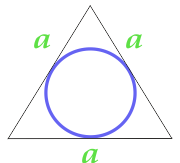
16
Areal af en cirkel, der er indskrevet i en isosceles trapezoid, beregnet ud fra basen af trapezoidet og vinklen ved basen
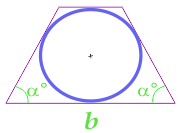
17
Området med cirklen beskrevet i nærheden af den ensartede trapezoid, beregnet på siderne af trapezoidet, dens diagonal og base
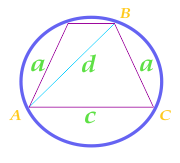
For at beregne arealet af en cirkel beregnes foreløbigt trekantens semiperimeter ABC
18
Området med cirklen beskrevet nær rektanglet
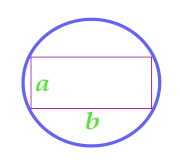
19
Areal af en cirkel beskrevet nær en almindelig polygon
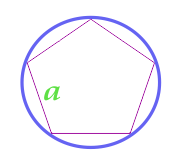
20
Areal af en cirkel beskrevet nær en almindelig sekskant
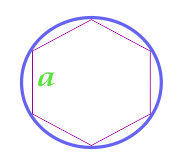
Bemærk:
Hvis vinklen i kildedataene er angivet i radianer, kan du bruge formlen til konvertering til grader: 1 radian ×
Tabel med formler for cirkelområdet
| indledende data (aktivt link for at gå til lommeregneren) |
skitse | formel | |
| 1 | radius |  |
|
| 2 | diameter |  |
|
| 3 | omkreds |  |
|
| 4 | side af en firkant |  |
|
| 5 | side af en firkant |  |
|
| 6 | side af trekanten |  |
hvor
|
| 7 | side af en ligesidet trekant |  |
|
| 8 | ligesidet trekanthøjde |  |
|
| 9 | side og base |  |
|
| 10 | side i højre vinkel på trekanten |  |
|
| 11 | side og base |  |
|
| 12 | sider og vinkel mellem dem |  |
|
| 13 | side af en højre trekant |  |
|
| 14 | side og vinkel i bunden af trekanten |  |
|
| 15 | side af en ligesidet trekant |  |
|
| 16 | side og vinkel i bunden af trapezoidet |  |
|
| 17 | trapesformens sider og diagonal |  |
hvor
|
| 18 | side af rektanglet |  |
|
| 19 | side og antal sider af polygonen |  |
|
| 20 | hexagon side |  |