L'aire du cercle
L'aire du cercle est la caractéristique numérique caractérisant le montant du plan, la ligne limitée de la circonférence. Calculer l'aire du cercle on peut avec l'aide du nombre de Pi et le rayon de la circonférence, ou avec l'aide d'autres données connues initiales. Notre calculatrice vous aidera gratuitement dans le régime en ligne calculer l'aire du cercle ou contrôler déjà les calculs accomplis.
Tableau avec les formules de l'aire du cercle (à la fin de la page)
1
L'aire du cercle dans le rayon
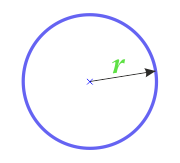
2
L'aire du cercle dans le diamètre

3
L'aire du cercle sur la longueur la circonférence

4
L'aire du cercle dans le carré inscrit dans le cercle

5
L'aire du cercle inscrit dans le carré
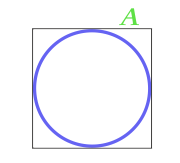
6
L'aire du cercle décrit près du triangle arbitraire
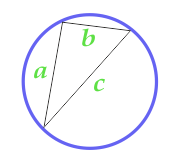
La formule donnée est employée seulement, si autour du triangle on peut décrire le cercle, c'est-à-dire tous trois sommets du triangle doivent être à la ligne de la circonférence. Le triangle peut être dans le cas présent chacun.
Pour le calcul de l'aire du cercle, nous compterons préalablement le semi-périmètre du triangle
7
L'aire du cercle décrit près du triangle équilatéral
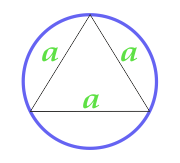
8
L'aire du cercle décrit près du triangle équilatéral, calculé en hauteur du triangle

9
L'aire du cercle décrit près du triangle isocèle
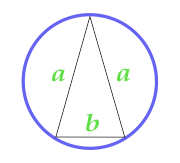
10
L'aire du cercle décrit près du triangle rectangle
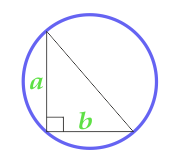
11
L'aire du cercle inscrit dans le triangle isocèle
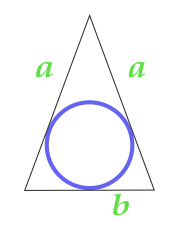
12
L'aire du cercle inscrit dans le triangle isocèle, calculé selon les côtés d'un triangle latéraux et l'angle entre eux
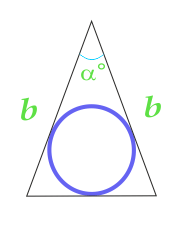
13
L'aire du cercle inscrit dans le triangle rectangle
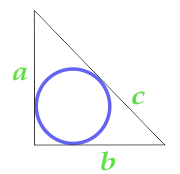
14
L'aire du cercle inscrit dans le triangle rectangle, calculé selon la partie et l'angle
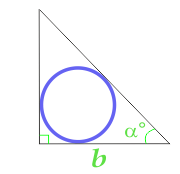
15
L'aire du cercle inscrit dans le triangle équilatéral
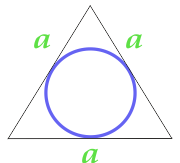
16
L'aire du cercle inscrit dans le trapèze isocèle, calculé selon la raison du trapèze et l'angle de base
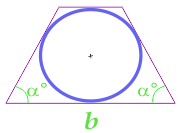
17
L'aire du cercle décrit près du trapèze isocèle, compté selon les parties latérales du trapèze, sa diagonale et la raison
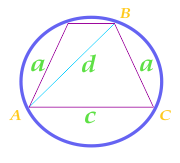
Pour le calcul de l'aire du cercle, nous compterons préalablement le semi-périmètre du triangle ABC
18
L'aire du cercle décrit près du rectangle
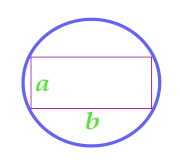
19
L'aire du cercle décrit près du polygone régulier
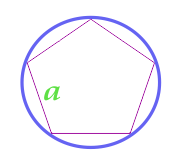
20
L'aire du cercle décrit près de l'hexagone juste
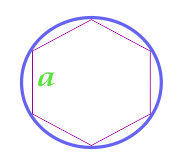
Remarque:
Si l'angle est en radians dans les données d'origine, vous pouvez utiliser la formule pour convertir en degrés: 1 radian × (180/π)° = 57,296°
Tableau avec les formules de l'aire du cercle
| données initiales (lien actif pour aller à la calculatrice) |
esquisse | formule | |
| 1 | Le rayon |  |
|
| 2 | Le diamètre |  |
|
| 3 | circonférence |  |
|
| 4 | côté de place |  |
|
| 5 | côté de place |  |
|
| 6 | côtés du triangle |  |
où
|
| 7 | côté du triangle équilatéral |  |
|
| 8 | hauteur du triangle équilatéral |  |
|
| 9 | côté et base |  |
|
| 10 | côtés à angle droit du triangle |  |
|
| 11 | côté et base |  |
|
| 12 | côtés et angle entre eux |  |
|
| 13 | côtés d'un triangle rectangle |  |
|
| 14 | côté et angle à la base du triangle |  |
|
| 15 | côté du triangle équilatéral |  |
|
| 16 | côté et angle à la base du trapèze |  |
|
| 17 | côtés et trapèze Diagonal |  |
où
|
| 18 | côtés du rectangle |  |
|
| 19 | côté et nombre de côtés du polygone |  |
|
| 20 | côté d'hexagone |  |