एक चक्र के क्षेत्र
एक चक्र के क्षेत्र में एक संख्यात्मक विशेषता की विशेषता है कि आकार के विमान से घिरा सर्कल लाइन है । क्षेत्र की गणना के चक्र का उपयोग किया जा सकता की संख्या PI और वृत्त की त्रिज्या, या का उपयोग अन्य ज्ञात स्रोत डेटा । हमारे कैलकुलेटर में मदद मिलेगी आप मुफ्त के लिए ऑनलाइन क्षेत्र की गणना के चक्र या गणना की जांच पहले से ही किया जाता है ।
सर्कल क्षेत्र फ़ार्मुलों के साथ तालिका (पृष्ठ के अंत में)
1
एक चक्र के क्षेत्र का उपयोग त्रिज्या
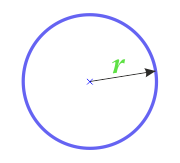
2
एक चक्र के क्षेत्र व्यास का उपयोग कर

3
क्षेत्र के एक वृत्त की परिधि

4
एक चक्र के क्षेत्र का उपयोग कर खुदा एक सर्कल में स्क्वायर

5
के क्षेत्र, एक सर्कल में खुदा एक वर्ग
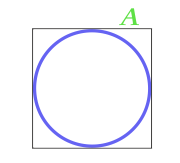
6
क्षेत्र के सर्किल वर्णित के बारे में एक मनमाना त्रिकोण
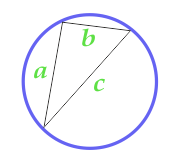
यह सूत्र लागू है, तो केवल एक वृत्त वर्णित किया जा सकता है चारों ओर के त्रिकोण, कि है, सभी तीन कोने के त्रिकोण झूठ चाहिए सर्कल लाइन पर. त्रिकोण में इस मामले में किसी भी हो सकता है ।
क्षेत्र की गणना करने के लिए, चक्र की गणना semiperimeter के त्रिकोण
7
क्षेत्र के सर्किल वर्णित के बारे में एक समबाहु त्रिभुज
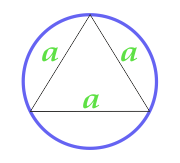
8
क्षेत्र के सर्किल वर्णित के बारे में एक समभुज त्रिकोण से गणना की ऊंचाई त्रिकोण

9
क्षेत्र के सर्किल वर्णित के पास समद्विबाहु त्रिकोण का
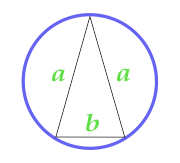
10
क्षेत्र के सर्किल वर्णित के बारे में एक सही त्रिकोण
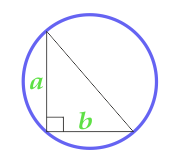
11
के क्षेत्र, एक सर्कल में खुदा एक समद्विबाहु त्रिकोण का
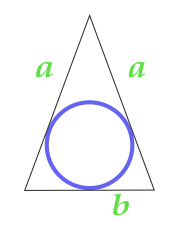
12
क्षेत्र के सर्कल में खुदा एक समद्विबाहु त्रिकोण पर गणना की है, दोनों पक्षों के त्रिकोण और उनके बीच के कोण
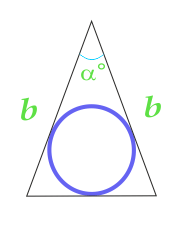
13
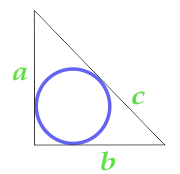
के क्षेत्र, एक सर्कल में खुदा एक त्रिकोण
14
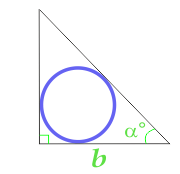
क्षेत्र के सर्कल में खुदा एक सही त्रिकोण की गणना की तरफ से और कोने
15
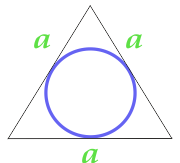
के क्षेत्र, एक सर्कल में खुदा एक समभुज त्रिकोण
16
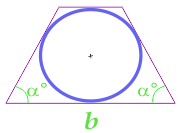
क्षेत्र के सर्कल में खुदा समद्विबाहु trapezoid, से गणना की चतुर्भुज के आधार और कोण के आधार पर
17
क्षेत्र के सर्किल वर्णित के पास समद्विबाहु trapezoid, गणना के पक्षों पर विषम चतुर्भुज, अपने विकर्ण और आधार
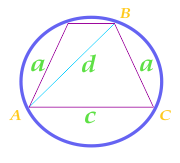
क्षेत्र की गणना करने के लिए, चक्र की गणना semiperimeter के त्रिकोण ABC
18
क्षेत्र के सर्किल वर्णित के पास आयत
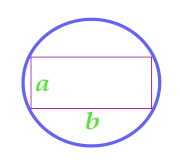
19
एक चक्र के क्षेत्र circumscribed के बारे में एक नियमित बहुभुज
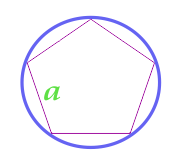
20
क्षेत्र के सर्किल वर्णित के बारे में एक नियमित रूप से hexagon
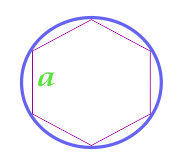
नोट:
कोण स्रोत डेटा में रेडियंस में सेट किया गया है, तो आप डिग्री करने के लिए इसे बदलने के लिए सूत्र का उपयोग कर सकते हैं: 1 रेडियन × (180/π)° = 57,296°
सर्कल क्षेत्र फ़ार्मुलों के साथ तालिका
| कच्चा डेटा (कैलकुलेटर पर जाने के लिए सक्रिय लिंक) |
एक स्केच | सूत्र | |
| 1 | त्रिज्या |  |
|
| 2 | व्यास |  |
|
| 3 | परिधि |  |
|
| 4 | एक वर्ग का |  |
|
| 5 | एक वर्ग का |  |
|
| 6 | त्रिभुज की तरफ |  |
जहाँ
|
| 7 | एक समबाहु त्रिभुज की ओर |  |
|
| 8 | समबाहु त्रिभुज ऊँचाई |  |
|
| 9 | ओर और आधार |  |
|
| 10 | त्रिभुज के समकोण पर पक्ष |  |
|
| 11 | ओर और आधार |  |
|
| 12 | उनके बीच के पक्ष और कोण |  |
|
| 13 | एक समकोण त्रिभुज की ओर |  |
|
| 14 | त्रिभुज के आधार पर पक्ष और कोण |  |
|
| 15 | एक समबाहु त्रिभुज की ओर |  |
|
| 16 | ट्रेपेज़ॉइड के आधार पर पक्ष और कोण |  |
|
| 17 | ट्रेपेज़ॉइड के पक्ष और विकर्ण |  |
जहाँ
|
| 18 | आयत का किनारा |  |
|
| 19 | पक्ष और बहुभुज के पक्षों की संख्या |  |
|
| 20 | षट्भुज पक्ष |  |