Daire alanı
Daire alanı, Daire çizgisi ile sınırlı bir düzlemin boyutunu karakterize eden sayısal bir özelliktir. Bir dairenin alanını Pi ve daire yarıçapını kullanarak veya bilinen diğer kaynak verileri kullanarak hesaplayabilirsiniz. Bizim hesap çevrimiçi Daire alanını hesaplamak veya zaten tamamlanan hesaplamalar kontrol etmek için ücretsiz size yardımcı olacaktır.
Daire alanı formüllü tablo (sayfanın sonunda)
1
Yarıçap boyunca Daire alanı
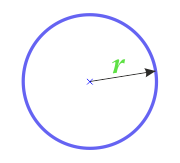
2
Çap boyunca Daire alanı

3
Çemberin uzunluğu boyunca Daire alanı

4
Daire ile Daire Kare

5
Kare içine yazılı Daire alanı
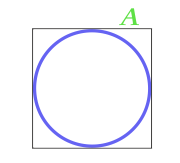
6
Rastgele bir üçgen hakkında açıklanan Daire alanı
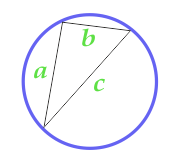
Bu formül yalnızca bir üçgenin etrafında bir daire tarif edilebilirse, yani üçgenin üç köşesinin Daire çizgisinde yatması gerekiyorsa geçerlidir. Bu durumda Üçgen herhangi biri olabilir.
Dairenin alanını hesaplamak için, üçgenin yarı ölçerini önceden hesaplarız
7
Eşkenar Üçgen hakkında açıklanan Daire alanı
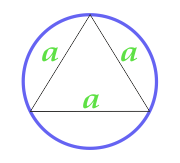
8
Üçgenin yüksekliği ile hesaplanan eşkenar Üçgen hakkında açıklanan Daire alanı

9
İkizkenar üçgeninin yakınında açıklanan Daire alanı
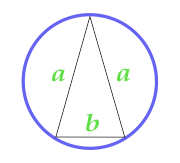
10
Dikdörtgen Üçgen hakkında açıklanan Daire alanı
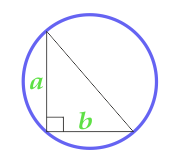
11
İkizkenar üçgenine yazılmış dairenin alanı
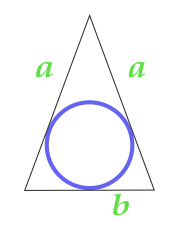
12
Dairenin alanı, üçgenin kenarlarında ve aralarındaki açıda hesaplanan ikizkenar üçgenine yazılır
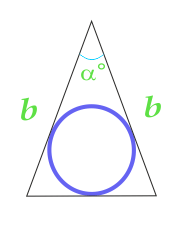
13
Dikdörtgen Üçgen içine yazılı Daire alanı
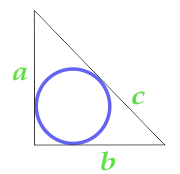
14
Yan ve köşe tarafından hesaplanan dikdörtgen Üçgen içine yazılı Daire alanı
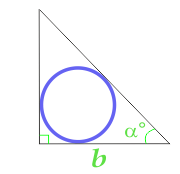
15
Eşkenar Üçgen içine yazılmış Daire alanı
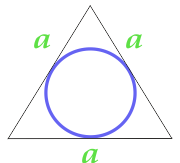
16
Tabanda trapez tabanına ve köşesine göre hesaplanan, ikizkenar yamuk içine yazılmış Daire alanı
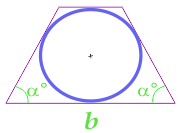
17
Trapezinin yan tarafında, köşegeninde ve tabanında hesaplanan bir trapezin yaklaşık olarak tarif edilen dairenin alanı
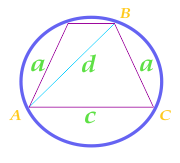
Dairenin alanını hesaplamak için, üçgenin yarı ölçerini önceden hesaplarız ABC
18
Dikdörtgen hakkında açıklanan Daire alanı
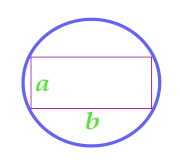
19
Doğru çokgen hakkında açıklanan Daire alanı
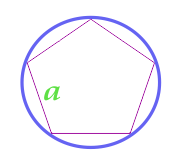
20
Doğru altıgen hakkında açıklanan Daire alanı
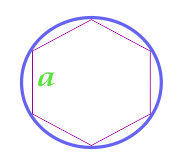
Not:
Orijinal verilerde açı radyan olarak ayarlanmışsa, derecelere çevirmek için formülü kullanabilirsiniz: 1 radyan × (180/π)° = 57,296°
Daire alanı formüllü tablo
| ham veri (hesap makinesine gitmek için etkin bağlantı) |
bir taslak | formül | |
| 1 | yarıçap |  |
|
| 2 | çap |  |
|
| 3 | çevre |  |
|
| 4 | bir meydanın tarafı |  |
|
| 5 | bir meydanın tarafı |  |
|
| 6 | üçgenin tarafı |  |
nerede
|
| 7 | eşkenar üçgenin tarafı |  |
|
| 8 | eşkenar üçgen yüksekliği |  |
|
| 9 | yan ve taban |  |
|
| 10 | üçgenin dik açısında yan |  |
|
| 11 | yan ve taban |  |
|
| 12 | yanlar ve aralarındaki açı |  |
|
| 13 | sağ üçgenin tarafı |  |
|
| 14 | üçgenin tabanında yan ve açı |  |
|
| 15 | eşkenar üçgenin tarafı |  |
|
| 16 | yamuk tabanındaki yan ve açı |  |
|
| 17 | yamuk kenarları ve köşegen |  |
nerede
|
| 18 | dikdörtgenin tarafı |  |
|
| 19 | çokgenin yanı ve kenar sayısı |  |
|
| 20 | altıgen taraf |  |