言語:
円の面積
円の面積は、円の線で囲まれた平面のサイズを特徴付ける数値特性です。 円の面積を計算するには、円の数と円の半径を使用するか、または他の既知のソースデータを使用することができます。 当社の卓までの無料オンライン計算の円またはチェックを計算しています。
円の面積の数式を含むテーブル (ページの最後に)
1
半径を使用した円の面積
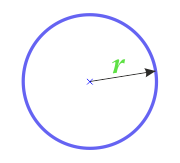
... トレーニング ...
r - 半径
2
直径を使用して円の面積

... トレーニング ...
D - 直径
3
円周率の面積

... トレーニング ...
- 円周
4
円の正方形に内接を使用して、円の面積

... トレーニング ...
a - パーティー
5
正方形に内接する円の面積
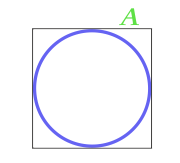
... トレーニング ...
A - パーティー
6
任意の三角形について説明されている円の面積
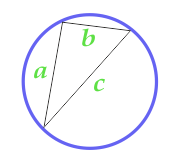
つまり、三角形の3つの頂点すべてが円線上にある必要があります。 この場合の三角形は任意です。
円の面積を計算するには、三角形の半周を計算します
... トレーニング ...
a - パーティー
b - パーティー
c - パーティー
7
円の面積は、正三角形について説明しました
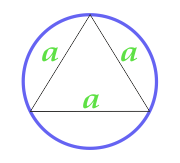
... トレーニング ...
a - パーティー
8
円の面積は、三角形の高さから計算された正三角形について説明されています

... トレーニング ...
h - 高度
9
二等辺三角形の近くに記載されている円の面積
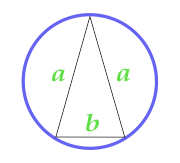
... トレーニング ...
a - パーティー
b - 財団
10
円の面積は、直角三角形について説明しました
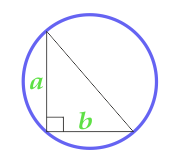
... トレーニング ...
a - パーティー
b - パーティー
11
二等辺三角形に内接する円の面積
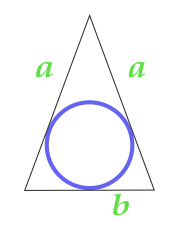
... トレーニング ...
a - パーティー
b - 財団
12
三角形の辺とそれらの間の角度で計算された、二等辺三角形に内接する円の面積
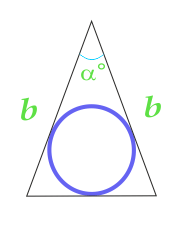
... トレーニング ...
b - パーティー
α - 辺の間の角度
13
直角三角形に内接する円の面積
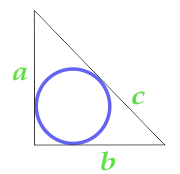
... トレーニング ...
a - パーティー
b - パーティー
c - パーティー
14
辺と角で計算された直角三角形に内接する円の面積
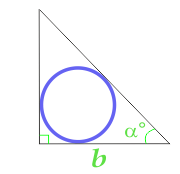
... トレーニング ...
b - パーティー
α - ベースでの角度
15
正三角形に内接する円の面積
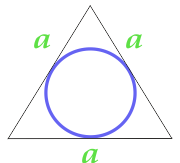
... トレーニング ...
a - パーティー
16
台形の底辺と底辺の角度から計算された、二等辺三角形に内接する円の面積
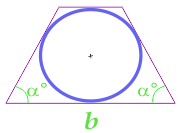
... トレーニング ...
b - パーティー
α - ベースでの角度
17
二等辺三角形の近くに記載されている円の面積台形、台形の辺、その対角線および底辺に計算される
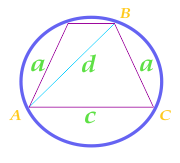
円の面積を計算するには、三角形の半周を計算します ABC
... トレーニング ...
a - パーティー
c - パーティー
d - 対角線
18
四角形の近くに記載されている円の面積
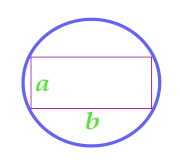
... トレーニング ...
a - パーティー
b - パーティー
19
正多角形について外接する円の面積
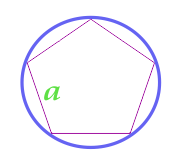
... トレーニング ...
a - パーティー
N - ポリゴンの辺の数
20
正六角形について説明した円の面積
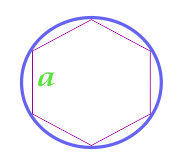
... トレーニング ...
a - パーティー
メモ:
角度がソースデータのラジアン単位で設定されている場合は、数式を使用して角度に変換できます: 1 ラジアン × (180/π)° = 57,296°
円の面積の数式を含むテーブル
| ソースデータ (電卓に行くためのアクティブリンク) |
スケッチ | 式 | |
| 1 | 半径 |  |
|
| 2 | 直径 |  |
|
| 3 | 円の長さ |  |
|
| 4 | 正方形の側面 |  |
|
| 5 | 正方形の側面 |  |
|
| 6 | 三角形の辺 |  |
どこに
|
| 7 | 正三角形の辺 |  |
|
| 8 | 正三角形の高さ |  |
|
| 9 | 側面および基盤 |  |
|
| 10 | 三角形の直角の辺 |  |
|
| 11 | 側面および基盤 |  |
|
| 12 | 辺とそれらの間の角度 |  |
|
| 13 | 直角三角形の辺 |  |
|
| 14 | 三角形の底辺の辺と角度 |  |
|
| 15 | 正三角形の辺 |  |
|
| 16 | 台形のベースの側面と角度 |  |
|
| 17 | 台形の辺と対角線 |  |
どこに
|
| 18 | 長方形の辺 |  |
|
| 19 | ポリゴンの辺と辺の数 |  |
|
| 20 | 六角形の側面 |  |