dil:
Üçgenin alanı
Alanın hesaplanması için üçgenler, formüller ve hesap makinesi alanı. eşkenar, ikizkenar ve dik açılı üçgenin belirli durumlar için üçgenler her türlü genel formülleri, Sağlar.
Üçgen alan formülleri içeren tablo (sayfanın sonunda)
Üçgen alan formüllerini resim veya dosya olarak indirin PDF (sayfanın sonunda)
Tüm üçgenler için
1
Üçgenin tabanı ve yüksekliği ile alanı
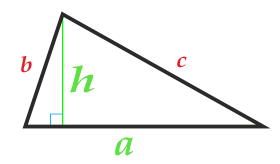
parti a
yükseklik h
Üçgenin tabanı üçgenin her iki tarafından da seçilebilir.
2
İki taraftaki üçgenin alanı ve aralarındaki açı
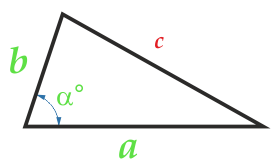
parti a
parti b
açı α° taraflar arasında a ve b
Taraflar arasındaki a açısı herhangi bir şey olabilir: künt, keskin, düz.
3
Yazılan çemberin yarıçapı boyunca üçgenin alanı ve üç kenarı
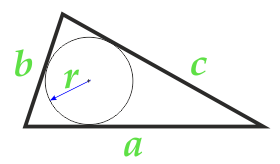
parti a
parti b
parti c
yarıçap r yazılı daire
4
Üçgenin çevresi ve üç kenarı boyunca üçgenin alanı
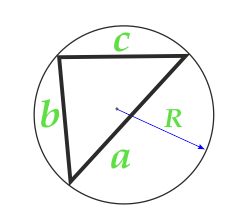
parti a
parti b
parti c
yarıçap R sınırlandırılmış çemberin
5
Heron formülüne göre üçgenin alanı
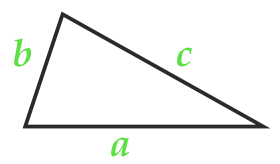
semiperimeter:
parti a
parti b
parti c
Yandaki isteğe bağlı üçgenin alanı ve iki bitişik köşe
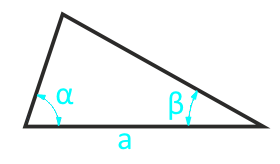
parti a
açı β°
açı α°
Isosceles üçgenler için
7
Yanlarda ve tabanda ikizkenar üçgen alanı
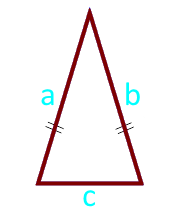
parti a (a = b)
parti c
8
Kenarları boyunca bir ikizkenar üçgenin alanı ve aralarındaki açı
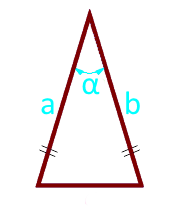
yan a (a = b)
açı α° iki taraf arasında
9
Kenarları boyunca bir ikizkenar üçgenin alanı ve aralarındaki açı
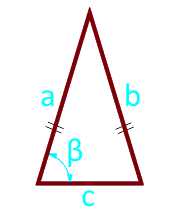
yan a (a = b)
Üçgenin tabanı c
açı β° baz ve yan arasında
10
Tabandaki bir ikizkenar üçgenin alanı ve kenarların arasındaki açı
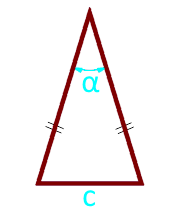
Üçgenin tabanı c
açı α° iki taraf arasında
Eşkenar üçgenler için
11
Bir ikizkenar üçgeni yüksekliği ve tabanı
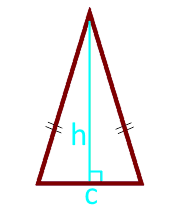
Üçgenin tabanı c
yükseklik h
12
Tarafta bir eşkenar üçgenin alanı
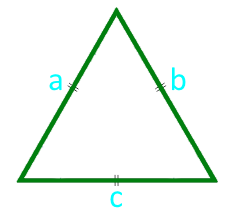
parti a (a = b = c)
13
Eşkenar üçgenin yüksekliği
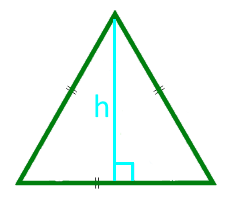
yükseklik h
14
Yazılan çemberin yarıçapı boyunca eşkenar üçgenin alanı
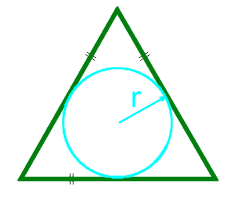
yarıçap r yazılı daire
15
Sınırlı çemberin yarıçapı boyunca eşkenar üçgenin alanı
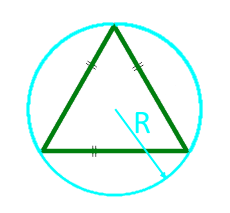
yarıçap R sınırlandırılmış çemberin
Sağ açılı üçgenler için
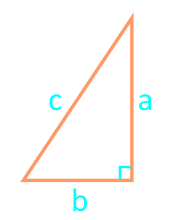
16
İki ayaklı bir sağ üçgenin karesi
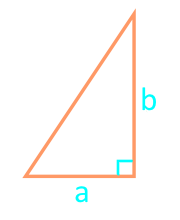
dik kenar a
dik kenar b
17
Hipotenüs ve açı ile dik bir üçgenin alanı
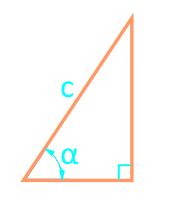
parti c
açı α
18
Bacak ve köşe boyunca dik üçgenin alanı
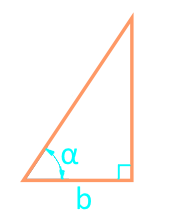
parti b
açı α
19
hipotenüs teğet çemberi bölen için segmentleri boyunca bir dik üçgen alanı
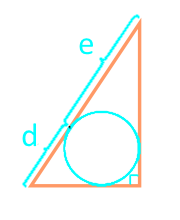
bölüm d
bölüm e
20
Hipotenüs ve yazıtlı daire boyunca dik açılı bir üçgenin alanı
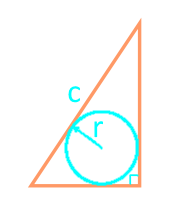
parti с
yarıçap r
21
Heron formülüne göre dik açılı bir üçgenin alanı
semiperimeter:
parti a
parti b
parti c
Üçgenin türüne ve bilinen kaynak verilerine bağlı olarak, üçgenin alanı çeşitli formüller kullanılarak hesaplanabilir.
Üçgen alan formülleri içeren tablo
| ham veri (hesap makinesine gitmek için etkin bağlantı) |
bir taslak | formül | |
| Tüm üçgenler için | |||
| 1 | taban ve yükseklik |  |
|
| 2 | iki taraf ve aralarındaki açı |  |
|
| 3 | daire yarıçapı ve üç tarafı |  |
|
| 4 | sınırlandırılmış dairenin yarıçapı ve üç tarafı |  |
|
| 5 |
üç taraf (Heron’un formülüne göre) |
 |
nerede
|
| 6 | yan ve iki bitişik köşe |  |
|
| Isosceles üçgenler için | |||
| 7 | yanlar ve taban |  |
|
| 8 | yanlar ve aralarındaki açı |  |
|
| 9 | yanlar, taban ve yanlar ve taban arasındaki açı |  |
|
| 10 | yanlar arasındaki taban ve açı |  |
|
| 11 | yükseklik ve taban |  |
|
| Eşkenar üçgenler için | |||
| 12 | parti |  |
|
| 13 | yükseklik |  |
|
| 14 | daire yarıçapı |  |
|
| 15 | sınırlandırılmış dairenin yarıçapı |  |
|
| Sağ açılı üçgenler için | |||
| 16 | iki bacak | 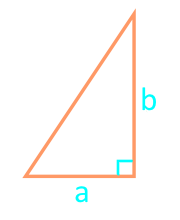 |
|
| 17 | hipotenüs ve açı |  |
|
| 18 | bacak ve köşe |  |
|
| 19 | içine alınmış dairenin hipotenusu böldüğü bölümler | 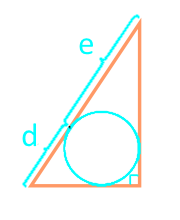 |
|
| 20 | hipotenüs ve yazılı daire yarıçapı |  |
|
| 21 |
üç taraf (Heron’un formülüne göre) |
 |
nerede
|





