език:
Лице на триъгълник
Лице на триъгълник - формули и калкулатор за изчисляване на областта онлайн. Дадени са общи формули за всички типове триъгълници, специални случаи за равностранен, равнобедрен и десен триъгълник.
Таблица с формули за квадрат на триъгълник (в края на страницата)
Изтеглете формулите за триъгълник като снимка или файл PDF (в края на страницата)
Лице на произволен триъгълник
1
Лице на триъгълник по неговата основа и височина
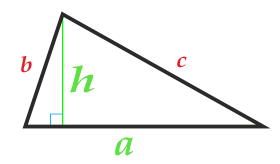
страна a
височина h
Базата на триъгълника може да бъде избрана от двете страни на триъгълника.
2
въведете стойност
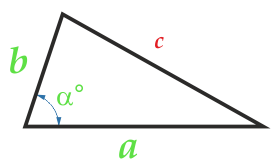
страна a
страна b
ъгъл α° между страните а и б
височина
3
средната линия
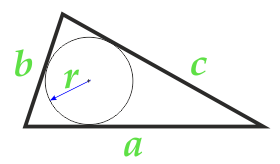
страна a
страна b
страна c
радиус r вписан кръг
4
радиус на вписанной обиколката
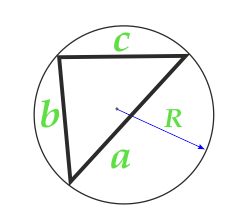
страна a
страна b
страна c
радиус R на окръжния кръг
5
основа
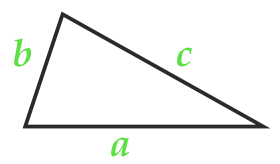
Решение:
страна a
страна b
страна c
Площта на произволен триъгълник отстрани и двата съседни ъгъла
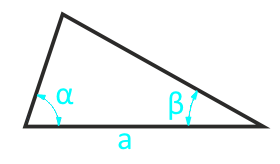
страна a
ъгъл β°
ъгъл α°
Отговор
7
Площта на равнобедрен триъгълник от двете страни и основата
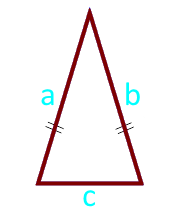
страна a (a = b)
страна c
8
периметър
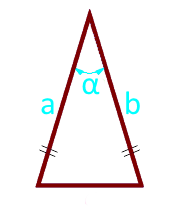
страната a (a = b)
ъгъл α° между страните
9
период от
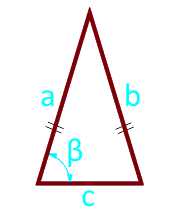
страната a (a = b)
Основата на триъгълника c
ъгъл β° подготовка
10
радиус на описаната окръжност
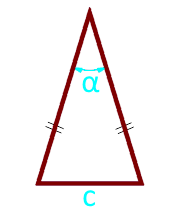
Основата на триъгълника c
ъгъл α° между страните
радиус
11
Площ на равнобедрен триъгълник по височина и основа
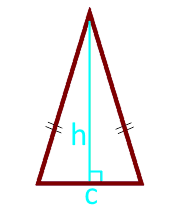
Основата на триъгълника c
височина h
12
диаметър
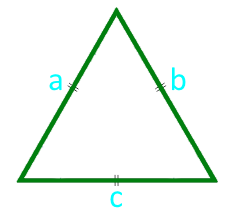
страна a (a = b = c)
13
Лице на равностранен триъгълник във височина
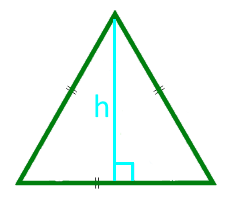
височина h
14
Лице на равностранен триъгълник по радиуса на вписания кръг
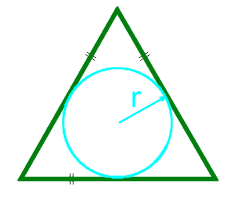
радиус r вписан кръг
15
Лице на равностранен триъгълник по радиуса на очертания кръг
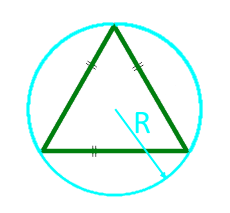
радиус R на окръжния кръг
Лице на правоъгълен триъгълник
16
Лице на правоъгълен триъгълник с два крака
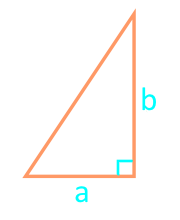
катет a
катет b
17
Площта на правоъгълен триъгълник през хипотенузата и ъгъла
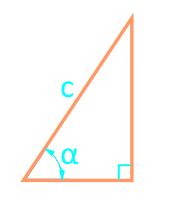
страна c
ъгъл α
18
Площ на правоъгълен триъгълник чрез ролка и ъгъл
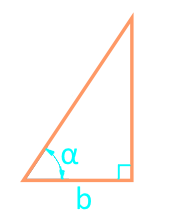
страна b
ъгъл α
19
Лице на правоъгълен триъгълник по сегментите, разделящи хипотенузата на вписан кръг
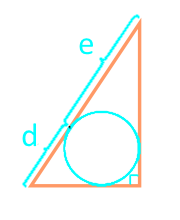
сегмент d
сегмент e
20
Площта на правоъгълен триъгълник през хипотенузата и вписаната окръжност
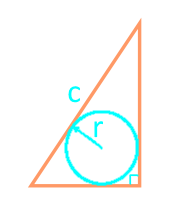
страна с
радиус r
21
Лице на правоъгълен триъгълник според формулата на Херон
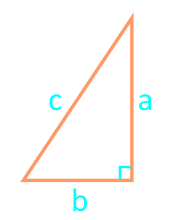
Решение:
страна a
страна b
страна c
В зависимост от вида на триъгълника и неговите известни изходни данни, площта на триъгълника може да се изчисли по различни формули.
Таблица с формули за квадрат на триъгълник
| данни (активна връзка за преминаване към калкулатор) |
миниатюра | формула | |
| Лице на произволен триъгълник | |||
| 1 | база и височина |  |
|
| 2 | двете страни и ъгълът между тях |  |
|
| 3 | радиус на вписана окръжност и три страни |  |
|
| 4 | радиус на описаната окръжност и три страни |  |
|
| 5 |
три страни (по формулата на Херона) |
 |
навсякъде
|
| 6 | страна и два съседни ъгъла |  |
|
| Отговор | |||
| 7 | страни и основа |  |
|
| 8 | страни и ъгъл между тях |  |
|
| 9 | страни, основа и ъгъл между страните и основата |  |
|
| 10 | основата и ъгълът между страните |  |
|
| 11 | височина и основа |  |
|
| радиус | |||
| 12 | страна |  |
|
| 13 | височина |  |
|
| 14 | радиус на вписаната окръжност |  |
|
| 15 | радиус на описаната окръжност |  |
|
| Лице на правоъгълен триъгълник | |||
| 16 | две ролки | 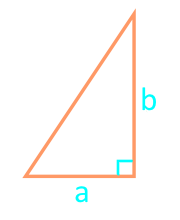 |
|
| 17 | хипотенузата и ъгълът |  |
|
| 18 | ъгъл и ъгъл |  |
|
| 19 | сегменти, в които се разделя вписаната окръжност на хипотенузата | 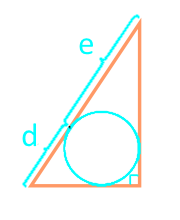 |
|
| 20 | хипотенузата и радиуса на вписаната окръжност |  |
|
| 21 |
три страни (по формулата на Херона) |
 |
навсякъде
|





