språk:
Arealet av trekanten
Område med trekanter, formler og kalkulator for beregning av område i online-modus. Gir generelle formler for alle typer trekanter, for spesielle tilfeller av likesidet, likebeint og rettvinklede trekanter.
Tabell med triangel formler (på slutten av siden)
Last ned trekantområdeformler som bilde eller fil PDF (på slutten av siden)
For alle trekanter
1
Arealet av trekanten ved base og høyde
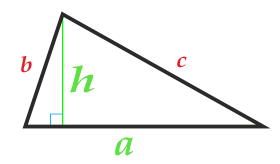
selskap a
høyde h
Trekantens base kan velges fra hver side av trekanten.
2
Arealet av trekanten på to sider og vinkelen mellom dem
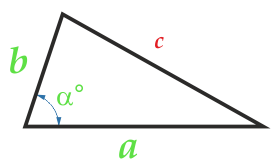
selskap a
selskap b
vinkel α° mellom partier a og b
Vinkelen a mellom sidene kan være alt: stump, skarp, rett.
3
Arealet av trekanten langs radiusen til den innskrevne sirkel og de tre sidene
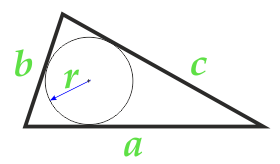
selskap a
selskap b
selskap c
radius r innskrevet sirkel
4
Området på trekanten langs radiusen til den omkretsede sirkelen og de tre sidene
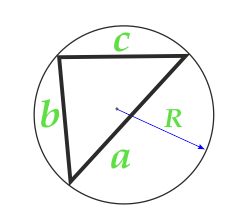
selskap a
selskap b
selskap c
radius R av den omtalte sirkelen
5
Arealet av trekanten ifølge Herons formel
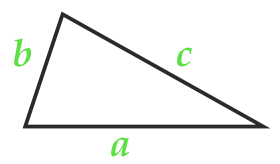
semiperimeter:
selskap a
selskap b
selskap c
Området på en vilkårlig trekant på siden og to tilstøtende hjørner
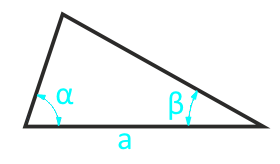
selskap a
vinkel β°
vinkel α°
For enslige triangler
7
Området likebent trekant på sidene og base
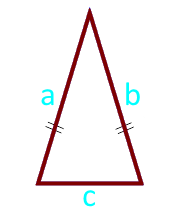
selskap a (a = b)
selskap c
8
Området av en liket trekant langs sidene og vinkelen mellom dem
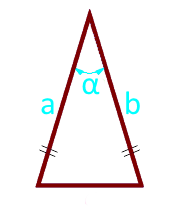
den siden a (a = b)
vinkel α° mellom sidene
9
Området av en liket trekant langs sidene og vinkelen mellom dem
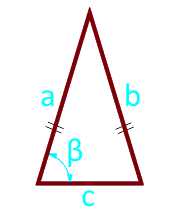
den siden a (a = b)
Basen av trekanten c
vinkel β° mellom base og side
10
Området av en likestilt trekant på basen og vinkelen mellom sidene
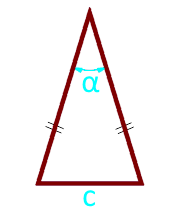
Basen av trekanten c
vinkel α° mellom sidene
For ekvilaterale trekanter
11
Arealet av en likebent trekant i høyde og base
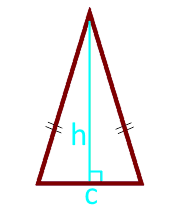
Basen av trekanten c
høyde h
12
Arealet av en like-sidig trekant på siden
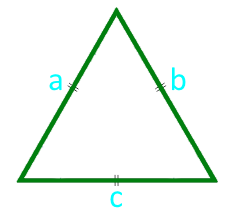
selskap a (a = b = c)
13
Arealet av en like-sidig trekant i høyden
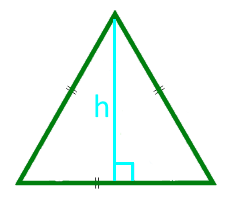
høyde h
14
Området av en like-sidig trekant langs radiusen til den innskrevne sirkelen
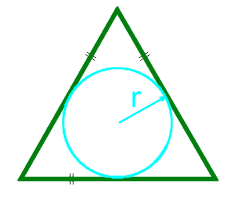
radius r innskrevet sirkel
15
Området av en like-sidig trekant langs radiusen til den omkretsede sirkelen
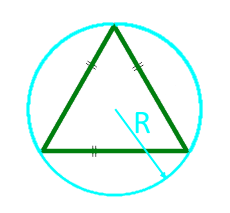
radius R av den omtalte sirkelen
For rettvinklede trekanter
16
Kvadrat av en riktig trekant med to ben
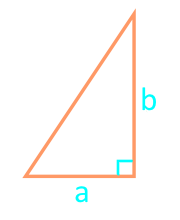
katet a
katet b
17
Området rett trekant gjennom hypotenuse og vinkel
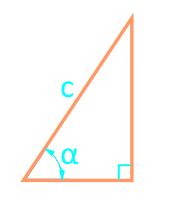
selskap c
vinkel α
18
Området rett trekant gjennom kateteret og vinkel
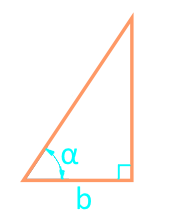
selskap b
vinkel α
19
Arealet av en rettvinklet trekant langs segmentene som deler hypotenusen i en innskrevet sirkel
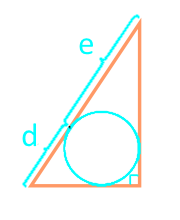
segment d
segment e
20
Området rett trekant gjennom hypotenuse og innskrevet sirkel
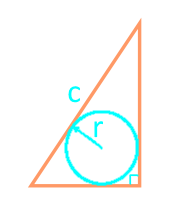
selskap с
radius r
21
Arealet av en rettvinklet trekant ifølge Herons formel
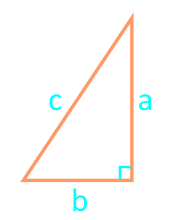
semiperimeter:
selskap a
selskap b
selskap c
Avhengig av trekanten, og det er kjent kilde for data, arealet av en trekant kan beregnes ved ulike formler.
Tabell med triangel formler
| kilde data (aktiv lenke for å gå til kalkulator) |
skisse | formelen | |
| For alle trekanter | |||
| 1 | base og høyde |  |
|
| 2 | to sider og vinkelen mellom dem |  |
|
| 3 | radius av innskrevet sirkel og tre sider |  |
|
| 4 | radius av omskrevet sirkel og tre sider |  |
|
| 5 |
tre sider (ifølge Heron's formel) |
 |
der
|
| 6 | side og to tilstøtende hjørner |  |
|
| For enslige triangler | |||
| 7 | sider og base |  |
|
| 8 | sider og vinkelen mellom dem |  |
|
| 9 | sider, base og vinkelen mellom sidene og base |  |
|
| 10 | base-og vinkelen mellom sidene |  |
|
| 11 | høyde og base |  |
|
| For ekvilaterale trekanter | |||
| 12 | side |  |
|
| 13 | høyde |  |
|
| 14 | radius av innskrevet sirkel |  |
|
| 15 | radius av omskrevet sirkel |  |
|
| For rettvinklede trekanter | |||
| 16 | to katetre | 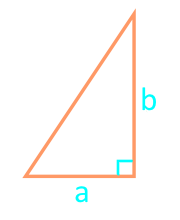 |
|
| 17 | den hypotenuse og vinkel |  |
|
| 18 | cathet og vinkel |  |
|
| 19 | segmentene inn som en innskrevet sirkel deler hypotenuse | 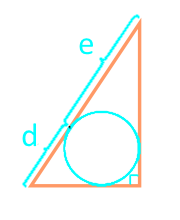 |
|
| 20 | hypotenuse og radius som er innskrevet sirkel |  |
|
| 21 |
tre sider (ifølge Heron's formel) |
 |
der
|





