Idioma:
Área de un triángulo
Área de un triángulo - fórmulas y calculadora para calcular el área online. Proporciona fórmulas generales para todos los tipos de triángulos, para casos particulares de equiláteros, isósceles y triángulos rectángulos.
Tabla con fórmulas de área triangular (al final de la página)
Descargue fórmulas de área triangular como una imagen o archivo PDF (al final de la página)
Para todos los triángulos
1
Área de un triángulo por su base y altura
Fiesta a
Altura h
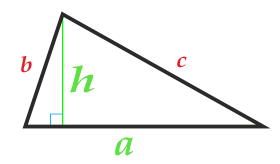
La base del triángulo se puede elegir de cualquier lado del triángulo.
2
Área de un triángulo en dos lados y el ángulo entre ellos
Fiesta a
Fiesta b
Ángulo α° entre las partes a y b
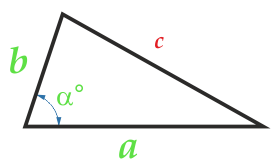
El ángulo α entre los lados puede ser cualquier cosa: contundente, agudo, recto.
3
Área de un triángulo a lo largo del radio del círculo inscrito y los tres lados
Fiesta a
Fiesta b
Fiesta c
Radio r círculo inscrito
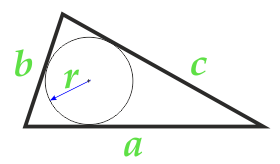
4
Área de un triángulo a lo largo del radio del círculo circunscrito y los tres lados
Fiesta a
Fiesta b
Fiesta c
Radio R del círculo circunscrito
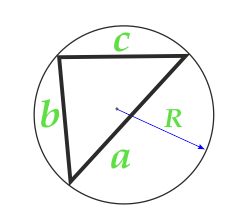
5
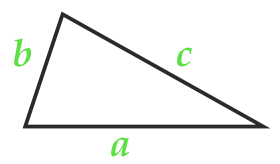
Área de un triángulo según la fórmula de Heron
Semiperímetro:
Fiesta a
Fiesta b
Fiesta c
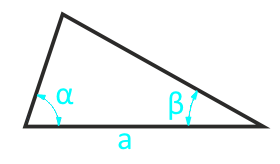
Área de un triángulo arbitrario en el costado y dos esquinas adyacentes.
Fiesta a
Ángulo β°
Ángulo α°
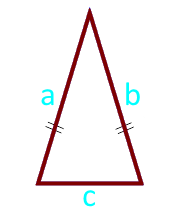
Para triángulos isósceles
7
El área del triángulo isósceles en los lados y la base.
Fiesta a (a = b)
Fiesta c
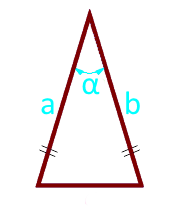
8
El área de un triángulo isósceles a lo largo de los lados y el ángulo entre ellos
Lado a (a = b)
Ángulo α° entre los lados
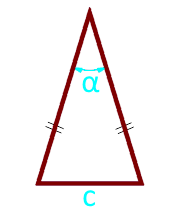
9
El área de un triángulo isósceles a lo largo de los lados y el ángulo entre ellos
Lado a (a = b)
La base del triángulo c
Ángulo β° entre la base y el costado
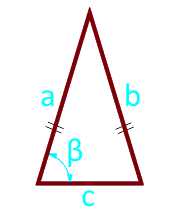
10
El área de un triángulo isósceles en la base y el ángulo entre los lados
La base del triángulo c
Ángulo α° entre los lados
Para triángulos equiláteros
11
El área de un triángulo isósceles en altura y base
La base del triángulo c
Altura h
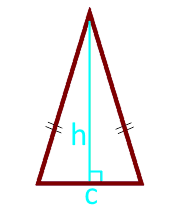
12
El área de un triángulo equilátero en el lado
Fiesta a (a = b = c)
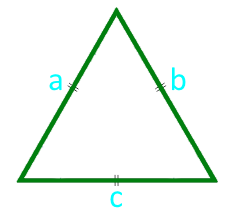
13
El área de un triángulo equilátero en altura
Altura h
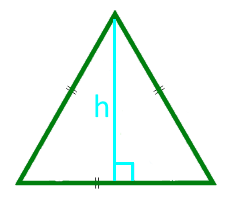
14
El área de un triángulo equilátero a lo largo del radio del círculo inscrito
Radio r círculo inscrito
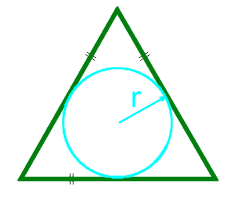
15
El área de un triángulo equilátero a lo largo del radio del círculo circunscrito
Radio R del círculo circunscrito
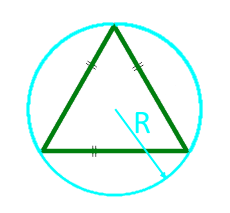
Para triángulos en ángulo recto
16
Cuadrado de un triángulo rectángulo con dos patas
Cathete a
Cathete b
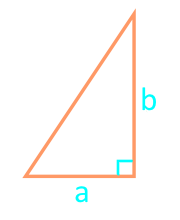
17
Área de un triángulo rectángulo a través de hipotenusa y ángulo
Fiesta c
Ángulo α
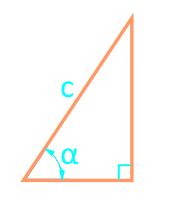
18
Área de un triángulo rectángulo a través de una pierna y ángulo
Fiesta b
Ángulo α
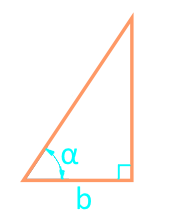
19
El área de un triángulo rectángulo largo de los segmentos para los cuales la hipotenusa divide el círculo inscrito
Segmento d
Segmento e
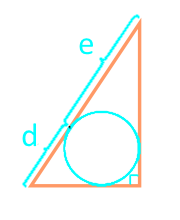
20
Área de un triángulo rectángulo a través de la hipotenusa y el círculo inscrito
Fiesta с
Radio r
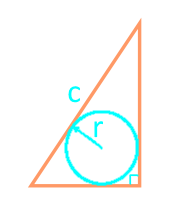
21
El área de un triángulo rectángulo utilizando la fórmula de Heron
Semiperímetro:
Fiesta a
Fiesta b
Fiesta c
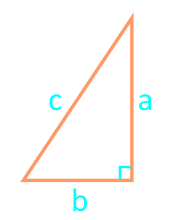
Dependiendo del tipo de triángulo y sus datos fuente conocidos, el área del triángulo se puede calcular usando varias fórmulas.
Tabla con fórmulas de área triangular
| datos en bruto (enlace activo para ir a la calculadora) |
un boceto | la formula | |
| Para todos los triángulos | |||
| 1 | base y altura | |
|
| 2 | dos lados y el ángulo entre ellos | |
|
| 3 | radio circular y tres lados | |
|
| 4 | radio del círculo circunscrito y tres lados | |
|
| 5 |
tres lados (de acuerdo con la fórmula de Heron) |
|
donde
|
| 6 | lateral y dos esquinas adyacentes | |
|
| Para triángulos isósceles | |||
| 7 | lados y base | |
|
| 8 | lados y ángulo entre ellos | |
|
| 9 | lados, base y ángulo entre lados y base | |
|
| 10 | base y ángulo entre los lados | |
|
| 11 | altura y base | |
|
| Para triángulos equiláteros | |||
| 12 | lado | |
|
| 13 | altura | |
|
| 14 | radio circular | |
|
| 15 | radio del círculo circunscrito | |
|
| Para triángulos en ángulo recto | |||
| 16 | dos piernas | |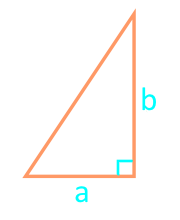
|
| 17 | hipotenusa y angulo | |
|
| 18 | pierna y esquina | |
|
| 19 | segmentos en los que el círculo inscrito divide la hipotenusa | |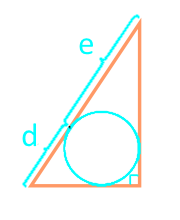
|
| 20 | hipotenusa y radio circular inscrito | |
|
| 21 |
tres lados (de acuerdo con la fórmula de Heron) |
|
donde
|
Descargue las fórmulas del área del triángulo como una imagen
