Aire d'un triangle
Aire d'un triangle - formules et calculatrice pour calculer la surface en mode en ligne. Des formules générales pour tous les types de triangles, des cas spéciaux pour les triangles équilatéraux, isocèles et rectangulaires sont donnés.
Tableau avec les formules de surface du triangle (à la fin de la page)
Téléchargez les formules de zones triangulaires sous forme d'image ou de fichier PDF (à la fin de la page)
Pour tous les triangles
1
Aire d'un triangle par sa base et sa hauteur
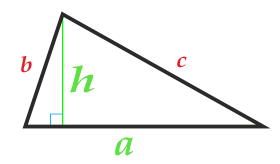
La base du triangle peut être choisie de chaque côté du triangle.
2
Aire d'un triangle sur deux côtés et l'angle entre eux
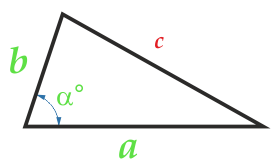
L'angle α entre les côtés peut être n'importe quoi: émoussé, pointu, droit.
3
Aire d'un triangle le long du rayon du cercle inscrit et des trois côtés
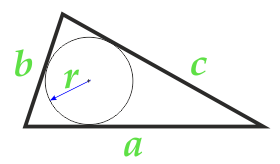
4
Aire d'un triangle le long du rayon du cercle circonscrit et des trois côtés
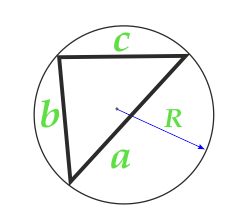
5
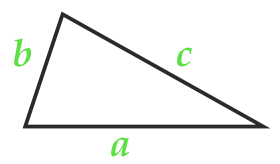
Aire d'un triangle selon la formule de Heron
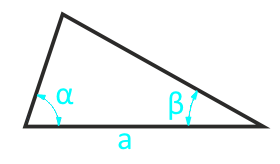
L'aire d'un triangle arbitraire sur le côté et les deux angles adjacents
Pour les triangles isocèles
7
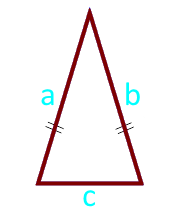
Surface du triangle isocèle sur les côtés et la base
8
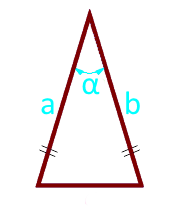
La zone d'un triangle isocèle le long des côtés et l'angle entre eux
9
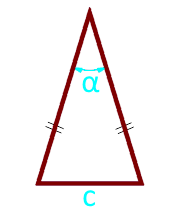
La zone d'un triangle isocèle le long des côtés et l'angle entre eux
10
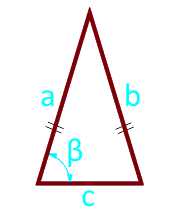
L'aire d'un triangle isocèle sur la base et l'angle entre les côtés
Pour les triangles équilatéraux
11
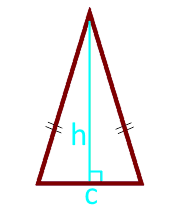
Aire d'un triangle isocèle en hauteur et en base
12
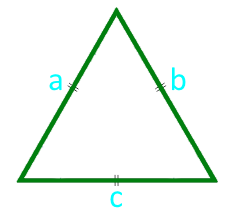
L'aire d'un triangle équilatéral sur le côté
13
L'aire d'un triangle équilatéral en hauteur
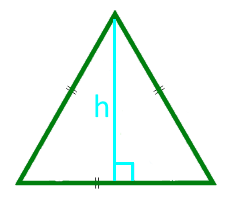
14
L'aire d'un triangle équilatéral le long du rayon du cercle inscrit
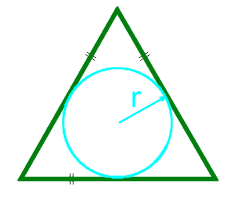
15
L'aire d'un triangle équilatéral le long du rayon du cercle circonscrit
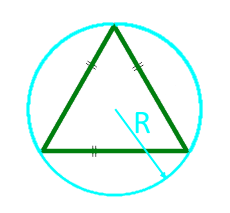
Pour les triangles rectangles
16
Carré d'un triangle rectangle avec deux jambes
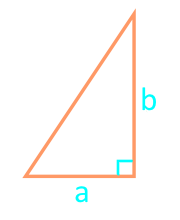
17
Zone d'un triangle rectangle à travers l'hypoténuse et l'angle
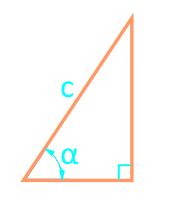
18
Zone d'un triangle rectangle à travers la jambe et l'angle
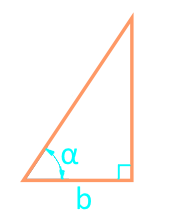
19
L'aire d'un triangle rectangle le long des segments divisant l'hypoténuse en un cercle inscrit
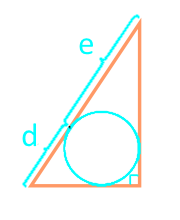
20
L'aire d'un triangle rectangle à travers l'hypoténuse et le cercle inscrit
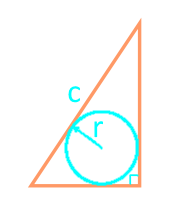
21
L'aire d'un triangle rectangle selon la formule de Heron
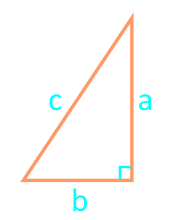
En fonction du type de triangle et de ses données d'origine connues, l'aire du triangle peut être calculée à partir de différentes formules.
Tableau avec les formules de surface du triangle
| données initiales (lien actif pour aller à la calculatrice) |
esquisse | formule | |
| Pour tous les triangles | |||
| 1 | base et hauteur | |
|
| 2 | deux côtés et un angle entre eux | |
|
| 3 | rayon du cercle inscrit et trois côtés | |
|
| 4 | rayon du cercle décrit et trois côtés | |
|
| 5 |
trois côtés (selon la formule de Gérone) |
|
où
|
| 6 | côté et deux angles adjacents | |
|
| Pour les triangles isocèles | |||
| 7 | côtés et base | |
|
| 8 | côtés et angle entre eux | |
|
| 9 | côtés, base et angle entre les côtés et la base | |
|
| 10 | base et angle entre les côtés | |
|
| 11 | hauteur et base | |
|
| Pour les triangles équilatéraux | |||
| 12 | côté | |
|
| 13 | hauteur | |
|
| 14 | rayon du cercle inscrit | |
|
| 15 | rayon du cercle décrit | |
|
| Pour les triangles rectangles | |||
| 16 | deux jambes | |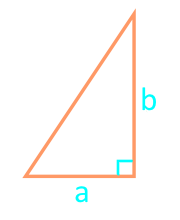
|
| 17 | hypoténuse et angle | |
|
| 18 | catet et angle | |
|
| 19 | segments en lesquels l'hypoténuse divise le cercle inscrit | |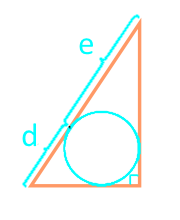
|
| 20 | hypoténuse et rayon du cercle inscrit | |
|
| 21 |
trois côtés (selon la formule de Gérone) |
|
où
|
Téléchargez les formules de zones triangulaires comme une image
