limbă:
Zona triunghiului
Zona de triunghiuri, formule și calculator pentru calcularea zonei în modul online. Oferă formule generale pentru toate tipurile de triunghiuri, pentru cazuri particulare de echilateral, isoscel și triunghiuri unghi drept.
Tabel cu formule de zonă triunghi (la sfârșitul paginii)
Descărcați formule de zonă triunghi ca imagine sau fișier PDF (la sfârșitul paginii)
Pentru toate triunghiurile
1
Suprafața triunghiului cu baza și înălțimea sa
petrecere a
înălțime h
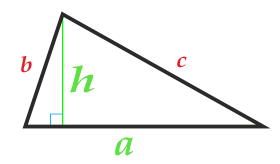
Baza triunghiului poate fi aleasă din ambele părți ale triunghiului.
2
Zona triunghiului pe două laturi și unghiul dintre ele
petrecere a
petrecere b
unghi α° între părțile a și b
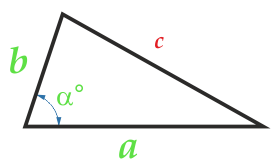
Unghiul α între laturi poate fi orice: blunt, ascuțit, drept.
3
Zona triunghiului de-a lungul razei cercului inscripționat și a celor trei laturi
petrecere a
petrecere b
petrecere c
rază r inscripționat cercul
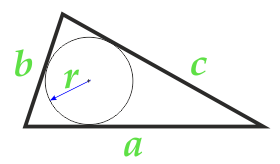
4
Zona triunghiului de-a lungul razei cercului circumscris și a celor trei laturi
petrecere a
petrecere b
petrecere c
rază R din cercul circumscris
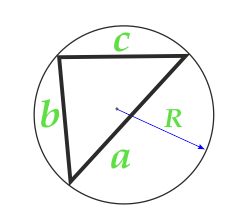
5
Zona triunghiului conform formulei lui Heron
semiperimetrul:
petrecere a
petrecere b
petrecere c
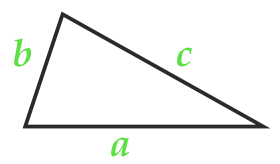
Zona unui triunghi arbitrar pe lateral și două colțuri adiacente
petrecere a
unghi β°
unghi α°
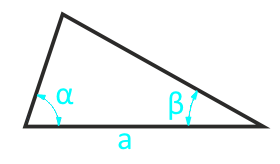
Pentru triunghiurile isoscel
7
Zona triunghiului izoscel pe laturi și bază
petrecere a (a = b)
petrecere c
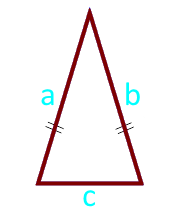
8
Suprafața unui triunghi isoscel de-a lungul laturilor și unghiul dintre ele
partea a (a = b)
unghi α° între părți
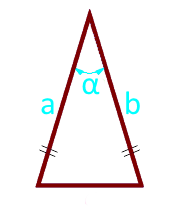
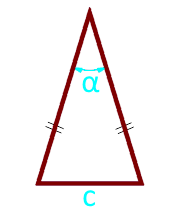
9
Suprafața unui triunghi isoscel de-a lungul laturilor și unghiul dintre ele
partea a (a = b)
Baza triunghiului c
unghi β° între bază și lateral
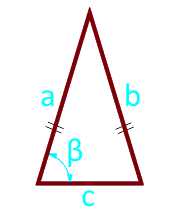
10
Zona unui triunghi isoscel la baza și unghiul dintre laturi
Baza triunghiului c
unghi α° între părți
Pentru triunghiuri echilaterale
11
Zona unui triunghi isoscel în înălțime și bază
Baza triunghiului c
înălțime h
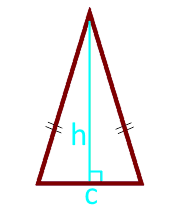
12
Zona unui triunghi echilateral pe lateral
petrecere a (a = b = c)
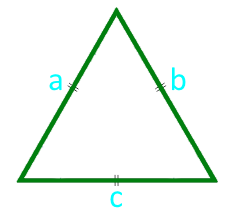
13
Zona unui triunghi echilateral în înălțime
înălțime h
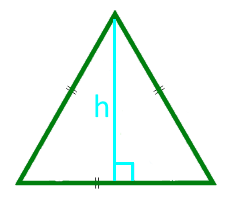
14
Zona unui triunghi echilateral de-a lungul razei cercului înscris
rază r inscripționat cercul
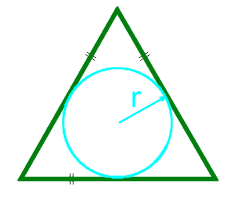
15
Zona unui triunghi echilateral de-a lungul razei cercului circumscris
rază R din cercul circumscris
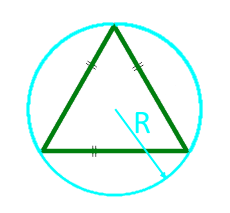
Pentru triunghiuri în unghi drept
16
Pătrat al unui triunghi drept cu două picioare
catetă a
catetă b
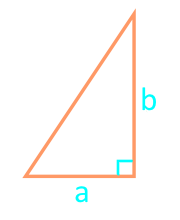
17
Zona unui triunghi drept prin hipotenuză și unghi
petrecere c
unghi α
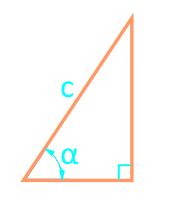
18
Zona unui triunghi drept printr-un picior și un colț
petrecere b
unghi α
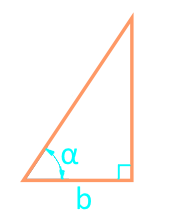
19
Zona unui triunghi dreptunghic de-a lungul segmentelor pentru care ipotenuza împarte cercul înscris
segment d
segment e
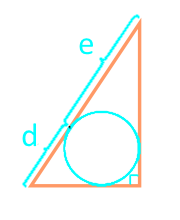
20
Zona unui triunghi unghi drept prin hipotenuză și cercul înscris
petrecere с
rază r
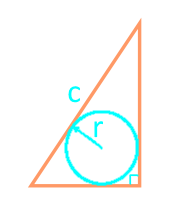
21
Zona unui triunghi în unghi drept în conformitate cu formula lui Heron
semiperimetrul:
petrecere a
petrecere b
petrecere c
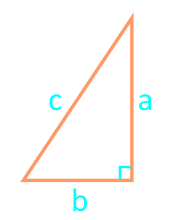
În funcție de tipul de triunghi și de datele sale sursă cunoscute, aria triunghiului poate fi calculată folosind diferite formule.
Tabel cu formule de zonă triunghi
| date brute (link activ pentru a merge la calculator) |
o schiță | formula | |
| Pentru toate triunghiurile | |||
| 1 | baza și înălțimea | |
|
| 2 | două părți și unghiul dintre ele | |
|
| 3 | raza cercului și trei laturi | |
|
| 4 | raza cercului circumscris și trei laturi | |
|
| 5 |
trei laturi (conform formulei lui Heron) |
|
unde
|
| 6 | lateral și două colțuri adiacente | |
|
| Pentru triunghiurile isoscel | |||
| 7 | laturile și baza | |
|
| 8 | laturile și unghiul dintre ele | |
|
| 9 | laturile, baza și unghiul dintre laturi și bază | |
|
| 10 | baza și unghiul dintre laturi | |
|
| 11 | inaltime si baza | |
|
| Pentru triunghiuri echilaterale | |||
| 12 | petrecere | |
|
| 13 | înălțime | |
|
| 14 | raza cercului | |
|
| 15 | raza cercului circumscris | |
|
| Pentru triunghiuri în unghi drept | |||
| 16 | două picioare | |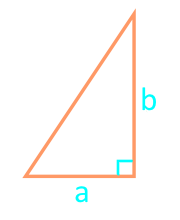
|
| 17 | hipotenuză și unghi | |
|
| 18 | piciorul și colțul | |
|
| 19 | segmente în care cercul înscris împarte hipotenuză | |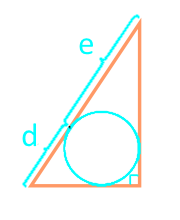
|
| 20 | hipotenuză și raza cercului înscris | |
|
| 21 |
trei laturi (conform formulei lui Heron) |
|
unde
|
Descarcă formule de zonă triunghi ca imagine
