Area of a triangle
Area of a triangle, formulas for calculating the area of various types of triangles depending on the known source data, a calculator for finding the area online and a table with the area formulas of the triangles.
Table with triangle area formulas (at the end of the page)
Download triangle area formulas as a picture or file PDF (at the end of the page)
For all triangles
1
Area of triangle by its base and height
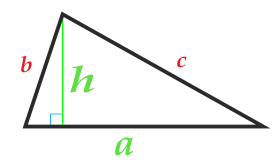
The triangle's base can be chosen from either side of the triangle.
2
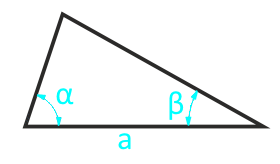
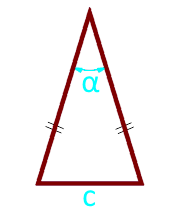
Area of triangle on two sides and the angle between them
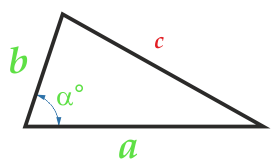
The angle α between the sides can be anything: blunt, sharp, straight.
3
Area of triangle along the radius of the inscribed circle and the three sides
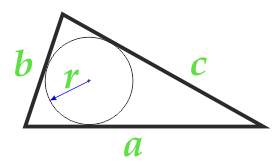
4
Area of triangle along the radius of the circumscribed circle and the three sides

5
Area of triangle according to Heron's formula
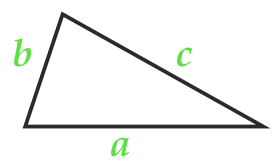
Area of an arbitrary triangle on the side and two adjacent corners
For isosceles triangles
7
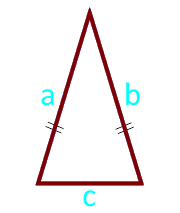
The area of the isosceles triangle on the sides and base
8
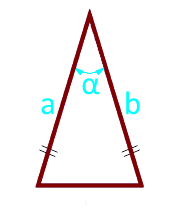
Area of an isosceles triangle along the sides and the angle between them
9
Area of an isosceles triangle on the side, base and angle between them
10
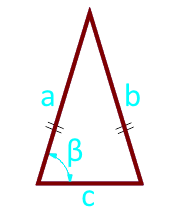
Area of an isosceles triangle on the base and angle between the sides
For equilateral triangles
11
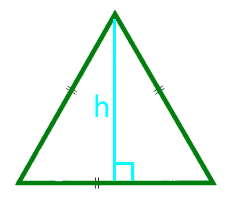
The area of an isosceles triangle in height and base

12
Area of an equilateral triangle on the side

13
Area of an equilateral triangle in height
14
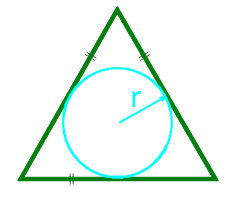
Area of an equilateral triangle along the radius of the inscribed circle
15
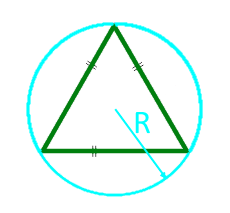
Area of an equilateral triangle along the radius of the circumscribed circle
For right-angled triangles
16
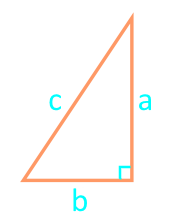
Square of a right triangle with two legs
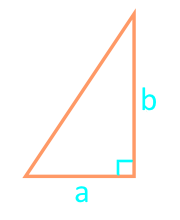
17
Area of a right triangle through hypotenuse and angle
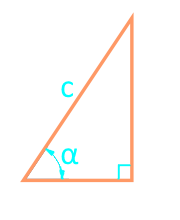
18
Area of a right-angled triangle through a leg and angle

19
Area of a right-angled triangle along the segments dividing the hypotenuse into an inscribed circle
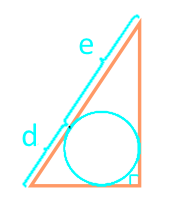
20
Area of a right-angled triangle through the hypotenuse and inscribed circle
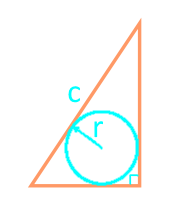
21
Area of a right-angled triangle according to Heron's formula
Our calculator for calculating the area will help you calculate the area of different types of triangles or check the already performed calculations.
Various formulas are used to calculate the area of a triangle, depending on the known input data. Above are formulas and a calculator that will help calculate the area of a triangle or check already performed calculations. General formulas are given for all types of triangles, special cases for equilateral, isosceles and right triangles.
Depending on the type of triangle and its known source data, the area of the triangle can be calculated using various formulas.
Table with triangle area formulas
| initial data (active link to go to the calculator) |
sketch | formula | |
| For all triangles | |||
| 1 | base and height |  |
|
| 2 | two sides and the angle between them |  |
|
| 3 | circle radius and three sides |  |
|
| 4 | radius of the circumscribed circle and three sides |  |
|
| 5 |
three sides (according to Heron’s formula) |
 |
Where
|
| 6 | side and two adjacent corners |  |
|
| For isosceles triangles | |||
| 7 | sides and base |  |
|
| 8 | sides and angle between them |  |
|
| 9 | sides, base and angle between sides and base |  |
|
| 10 | base and angle between the sides |  |
|
| 11 | height and base |  |
|
| For equilateral triangles | |||
| 12 | side |  |
|
| 13 | height |  |
|
| 14 | circle radius |  |
|
| 15 | radius of the circumscribed circle |  |
|
| For right-angled triangles | |||
| 16 | two legs | 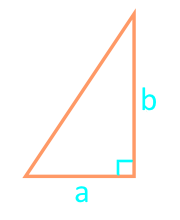 |
|
| 17 | hypotenuse and angle |  |
|
| 18 | leg and corner |  |
|
| 19 | segments into which the inscribed circle divides the hypotenuse | 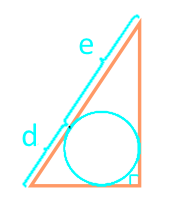 |
|
| 20 | hypotenuse and inscribed circle radius |  |
|
| 21 |
three sides (according to Heron’s formula) |
 |
Where
|
Definitions
The area of a triangle is a numerical characteristic characterizing the size of a plane limited by a geometric figure formed by three segments (sides) that connect three points (vertices) that do not lie on one straight line.
A triangle is a geometric figure formed by three segments that connect three points that are not lying on one straight line. The segments are called the sides of the triangle, and the points are the vertices of the triangle.
Area - is a numerical characteristic characterizing the size of a plane bounded by a closed geometric figure.
Area is measured in units of measurement squared: km2, m2, cm2, mm2, etc.





