Для студентов и школьников
Справочные материалы и различные калькуляторы по математике и другим дисциплинам для школьников и студентов высших учебных заведений. Информация о радиации доступным языком. Что такое радиация, ее виды и биологическое действие на человека.
А также другие материалы.
Наиболее популярные статьи:
Для студентов

Конвертер величин для перевода единиц измерения из одной величины в другую. С помощью конвертера можно быстро преобразовать различные физические величины и привести к требуемой единице измерения.

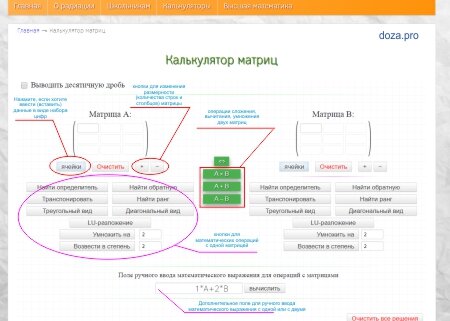
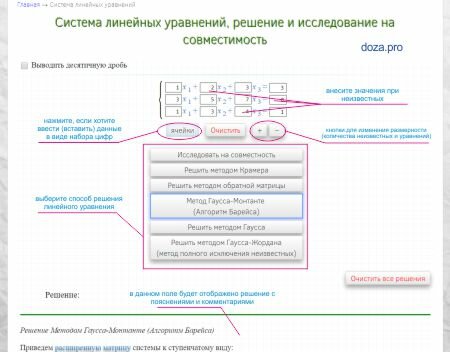
Вычислить определитель матрицы онлайн можно различными способами с помощью нашего сервиса. Решение бесплатное с пошаговыми действиями и пояснениями.

Основные тригонометрические тождества (равенства), формулы понижения степени, а также другие формулы.
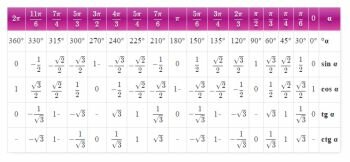
Таблица синусов, косинусов, тангенсов, котангенсов содержит вычисленные значения тригонометрических функций для определенного угла от 0 до 360 градусов.

Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.
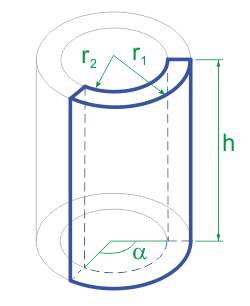
Вычисление объема и площади поверхностей части полого цилиндра, формулы и калькулятор для вычисления.
Для школьников

Формулы сокращенного умножения позволяют преобразовать математическое выражение к более простому для решения виду.

Тренажер таблицы умножения. Как помочь ребенку выучить таблицу. Распечатать или скачать таблицу нужного размера.

Таблица степеней чисел с 1 до 10. Калькулятор степеней онлайн. Интерактивная таблица и изображения таблицы степеней в высоком качестве.

Формулы и калькулятор, который поможет вычислить площадь треугольника или проверить уже выполненные вычисления.
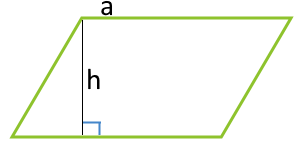
Для вычисления площади параллелограмма применяются различные формулы, в зависимости от известных исходных данных.
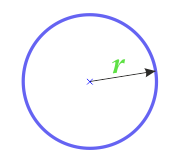
Наш калькулятор поможет вам бесплатно в режиме онлайн вычислить площадь круга или проверить уже выполненные вычисления.

Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.
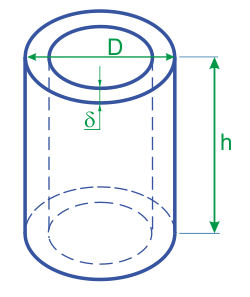
Объем полого цилиндра, формулы для вычисления объема и площадей правильного полого цилиндра.
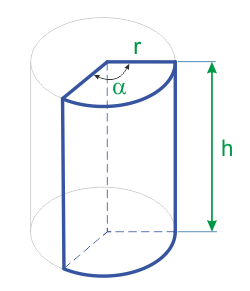
Вычисление объема и площади поверхностей части цилиндра, формулы и калькулятор для вычисления.
Статьи о радиации

Строение атома. Что такое радиация, причины возникновения радиации. Распад радиоактивных веществ. Что такое протоны, нейтроны, электроны, изотопы, нуклиды.

Источники радиации. Естественные источники излучения, природный радиационный фон. Космическая и солнечная радиация. Природные изотопы, радон, углерод 14 и калий 40.