Калькулятор матриц
Калькулятор матриц для пошагового решения матриц с последовательностью решения, бесплатно в режиме онлайн. Для всех вычислений приводятся пояснения и ссылки на необходимую теорию.
Решение:
Матричный калькулятор позволяет выполнить умножение матриц, сложение и вычитание матриц, найти ранг, вычислить определитель, осуществить транспонирование матрицы, найти обратную матрицу, а также выполнить другие операции с матрицами.
Наш калькулятор поможет выполнить математические операции с матрицами или проверить уже выполненные самостоятельно вычисления.
Описание калькулятора матриц
Используя калькулятор матриц, вы сможете выполнить необходимые вычисления с матрицами, получив в результате требуемый ответ и подробную последовательность решения. Матричный калькулятор позволяет выполнять операции с одной матрицей или решать сложные выражения сразу с несколькими матрицами.
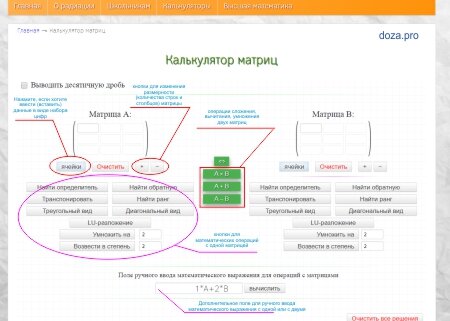
Заполните поля для элементов матрицы и нажмите соответствующую кнопку.
- С помощью плюса и минуса выберите нужный размер матрицы. Если нужна неквадратная матрица, то просто ненужные ячейки оставьте пустыми.
- Внесите значение элементов матрицы в ячейки. Значения могут быть:
- целые числа:
7,-3,0 - десятичные (конечные и периодические) дроби:
7/8,6.13,-1.3(56),1.2e-4 - арифметические выражения:
1/2+3*(6-4),(6-y)/x^3,2^0.5
- целые числа:
- Нажмите на кнопку с названием нужной математической операции или в ручном режиме введите математическое выражение в специальное поле.
- Значения в результатах решения можно с помощью мышки перетаскивать на различные поля. Например, полученную матрицу можно перетащить на поле исходных данных, для дальнейшего решения.