Площадь параллелограмма
Площадь параллелограмма, формулы и калькулятор для вычисления площади в режиме онлайн.
Для вычисления площади параллелограмма применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор для вычисления площади в режиме онлайн.
Площадь параллелограмма – это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками (сторонами), у которой противоположные стороны попарно параллельны и равны между собой.
Таблица с формулами площади параллелограмма (в конце страницы)
1
Площадь параллелограмма по основанию и высоте параллелограмма
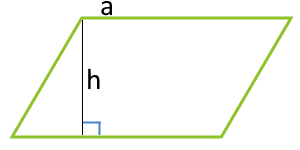
2
Площадь параллелограмма по стороне и высоте, опущенной на эту сторону
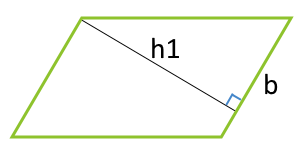
3
Площадь параллелограмма по двум сторонам и углу между ними
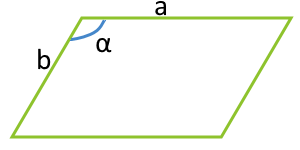
4
Площадь параллелограмма по двум диагоналям и углу между этими диагоналями
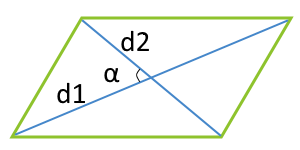
5
Площадь параллелограмма по вписанной окружности и стороне
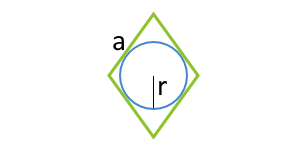
Данная формула применима только для параллелограммов, в которые можно вписать окружность. Таким параллелограммом может являться только ромб.
6
Площадь параллелограмма по вписанной окружности и углу между сторонами
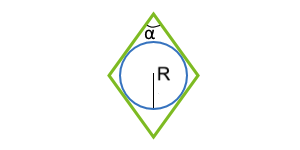
Данная формула применима только для параллелограммов, в которые можно вписать окружность. Таким параллелограммом может являться только ромб.
Примечание:
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади параллелограмма
| исходные данные (активная ссылка для перехода к калькулятору) |
эскиз | формула | |
| 1 | основание и высота |  |
|
| 2 |
сторона и высота, опущенная на эту сторону |
 |
|
| 3 | две стороны и угол между ними |  |
|
| 4 | диагонали и угол между ними |  |
|
| 5 | вписанная окружность и сторона |  |
|
| 6 | вписанная окружность и угол между сторонами |  |
Определения
Параллелограмм - это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами), у которой противоположные стороны попарно параллельны и равны между собой.
Высота параллелограмма – это отрезок проведенный из вершины параллелограмма к противоположной стороне под углом в 90 градусов.
Некоторые свойства параллелограмма:
- Сумма углов параллелограмма равна 360 градусов
- Сумма углов, прилегающих к любой из сторон равна 180 градусов
- Противоположные стороны параллельны и имеют одинаковую длину
- Противолежащие углы равны
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.