لغة:
منطقة متوازي الأضلاع
منطقة متوازي الأضلاع ، الصيغ وآلة حاسبة لحساب المنطقة على الخط. يتم إعطاء صيغ لحساب مساحة متوازي الأضلاع للعديد من البيانات الأولية.
جدول مع صيغ منطقة متوازية الأضلاع (في نهاية الصفحة)
1
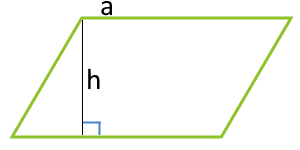
منطقة متوازي الأضلاع حسب القاعدة وارتفاع متوازي الأضلاع
... التدريب ...
a - الجانب
h - ارتفاع
2
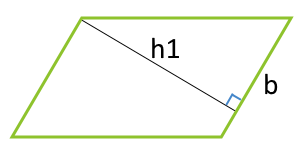
منطقة متوازي الأضلاع على طول الجانب والارتفاع خفضت لهذا الجانب
... التدريب ...
b - الجانب
hb - ارتفاع
3
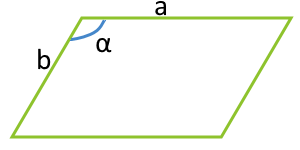
منطقة متوازي الأضلاع على الجانبين والزاوية بينهما
... التدريب ...
a - الجانب
b - الجانب
α° - الزاوية بين الجانبين
4
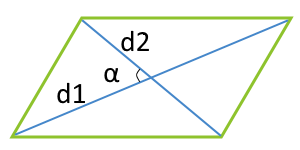
منطقة متوازي الأضلاع على طول القطرين والزاوية بين هذه الأقطار
... التدريب ...
d1 - قطري
d2 - قطري
α° - الزاوية بين الأقطار
5
منطقة متوازي الأضلاع على طول الدائرة المنقوشة والجانب
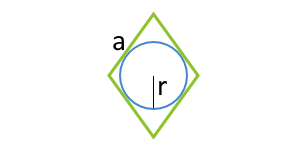
هذه الصيغة قابلة للتطبيق فقط على متوازيات الأضلاع ، حيث يمكن إدراج دائرة. يمكن لمثل متوازي الأضلاع أن يكون مجرد معين.
... التدريب ...
a - الجانب
r - نصف قطر الدائرة المدرج
6
منطقة متوازي الأضلاع على طول الدائرة المنقوشة والزاوية بين الجانبين
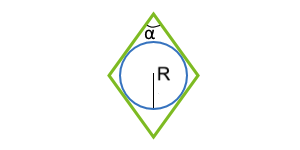
هذه الصيغة قابلة للتطبيق فقط على متوازيات الأضلاع ، حيث يمكن إدراج دائرة. يمكن لمثل متوازي الأضلاع أن يكون مجرد معين.
... التدريب ...
r - نصف قطر الدائرة المدرج
α° - الزاوية بين الجانبين
ملاحظة:
إذا الزاوية هو set بوصة مصدر البيانات أنت استخدام صيغة إلى تحويل الإيطالية إلى درجات:
1 radian × (180/π)° = 57,296°
جدول مع صيغ منطقة متوازية الأضلاع
| البيانات الخام (رابط نشط للذهاب إلى الآلة الحاسبة) |
رسم | الصيغة | |
| 1 | القاعدة والارتفاع |  |
|
| 2 | الجانب والارتفاع |  |
|
| 3 | وجهان والزاوية بينهما |  |
|
| 4 | الأقطار والزاوية بينهما |  |
|
| 5 | دائرة وجانب منقوش |  |
|
| 6 | دائرة وزاوية منقوشة بين الجانبين |  |