भाषा:
त्रिकोण का क्षेत्रफल
ऑनलाइन क्षेत्र की गणना के लिए त्रिकोण, सूत्र और कैलक्यूलेटर का क्षेत्र। त्रिकोण के सभी प्रकार के लिए सामान्य सूत्र, समभुज, समद्विबाहु और समकोण त्रिकोण के विशेष मामलों के लिए प्रदान करता है।
त्रिकोण क्षेत्र सूत्रों के साथ तालिका (पृष्ठ के अंत में)
चित्र या फ़ाइल के रूप में त्रिभुज क्षेत्र सूत्र डाउनलोड करें PDF (पृष्ठ के अंत में)
सभी त्रिकोणों के लिए
1
त्रिकोण का क्षेत्र इसके आधार और ऊंचाई से है
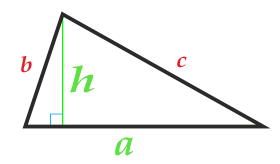
पार्टी a
ऊंचाई h
त्रिकोण के आधार को त्रिभुज के दोनों तरफ से चुना जा सकता है।
2
त्रिभुज का क्षेत्र दो तरफ और उनके बीच कोण
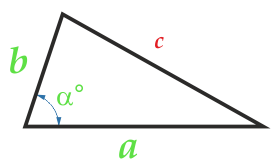
पार्टी a
पार्टी b
कोण α° पार्टियों ए और बी के बीच
किनारों के बीच कोण α कुछ भी हो सकता है: धुंधला, तेज, सीधे।
3
लिखित चक्र के त्रिज्या के साथ त्रिभुज का क्षेत्र और तीन तरफ
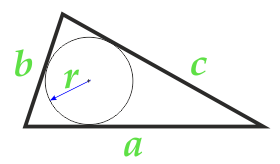
पार्टी a
पार्टी b
पार्टी c
त्रिज्या r अंकित सर्कल
4
परिपत्र सर्कल और तीन तरफ के त्रिज्या के साथ त्रिभुज का क्षेत्र
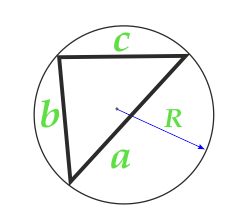
पार्टी a
पार्टी b
पार्टी c
त्रिज्या R सर्किल सर्कल का
5
हेरॉन के सूत्र के अनुसार त्रिभुज का क्षेत्रफल
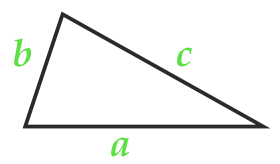
अर्द्धपरिधि:
पार्टी a
पार्टी b
पार्टी c
पक्ष और दो आसन्न कोनों पर एक मनमाना त्रिकोण का क्षेत्र
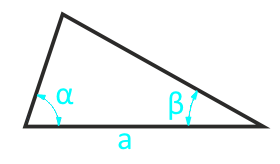
पार्टी a
कोण β°
कोण α°
Isosceles त्रिकोण के लिए
7
पक्षों और आधार पर समद्विबाहु त्रिभुज का क्षेत्रफल
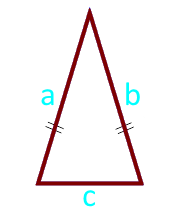
पार्टी a (a = b)
पार्टी c
8
पक्षों के साथ एक समद्विभुज त्रिभुज का क्षेत्र और उनके बीच कोण
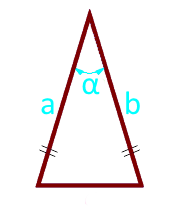
पक्ष a (a = b)
कोण α° पक्षों के बीच
9
पक्षों के साथ एक समद्विभुज त्रिभुज का क्षेत्र और उनके बीच कोण
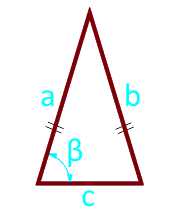
पक्ष a (a = b)
त्रिकोण का आधार c
कोण β° आधार और पक्ष के बीच
10
किनारे के बीच बेस और कोण पर एक समद्विभुज त्रिभुज का क्षेत्र
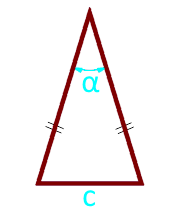
त्रिकोण का आधार c
कोण α° पक्षों के बीच
समतुल्य त्रिकोण के लिए
11
ऊँचाई और आधार में एक समद्विबाहु त्रिभुज का क्षेत्रफल
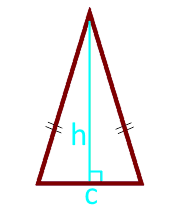
त्रिकोण का आधार c
ऊंचाई h
12
पक्ष में एक समतुल्य त्रिभुज का क्षेत्र
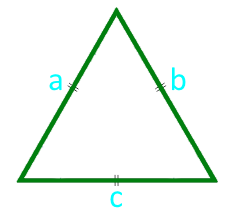
पार्टी a (a = b = c)
13
ऊंचाई में एक समतुल्य त्रिकोण का क्षेत्र
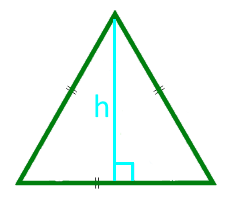
ऊंचाई h
14
अंकित चक्र के त्रिज्या के साथ एक समतुल्य त्रिभुज का क्षेत्र
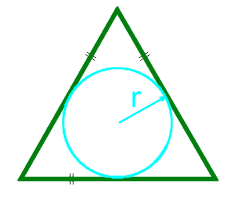
त्रिज्या r अंकित सर्कल
15
परिपत्र सर्कल के त्रिज्या के साथ एक समतुल्य त्रिभुज का क्षेत्र
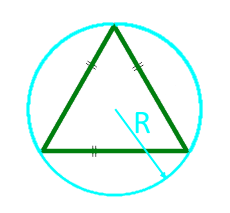
त्रिज्या R सर्किल सर्कल का
दाएं कोण वाले त्रिकोणों के लिए
16
दो पैरों के साथ एक सही त्रिकोण का स्क्वायर
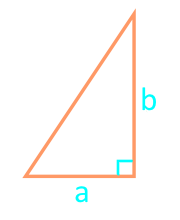
भुज a
भुज b
17
कर्ण और कोण के माध्यम से एक सही त्रिकोण का क्षेत्र
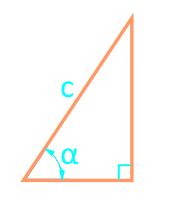
पार्टी c
कोण α
18
एक पैर और कोण के माध्यम से एक समकोण त्रिभुज का क्षेत्रफल
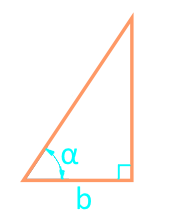
पार्टी b
कोण α
19
हाइपोटिन्यूज को एक लिखित सर्कल में विभाजित करने वाले खंडों के साथ दाएं कोण वाले त्रिभुज का क्षेत्र
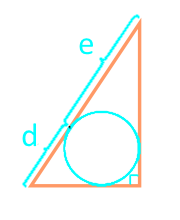
खंड d
खंड e
20
कर्ण और उत्कीर्ण वृत्त के माध्यम से एक समकोण त्रिभुज का क्षेत्रफल
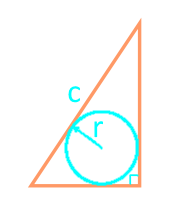
पार्टी с
त्रिज्या r
21
हेरॉन के सूत्र के अनुसार दाएं कोण वाले त्रिभुज का क्षेत्रफल
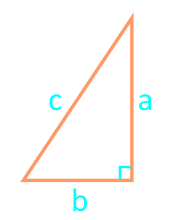
अर्द्धपरिधि:
पार्टी a
पार्टी b
पार्टी c
त्रिकोण के प्रकार और इसके ज्ञात स्रोत डेटा के आधार पर, विभिन्न सूत्रों का उपयोग करके त्रिकोण के क्षेत्र की गणना की जा सकती है।
त्रिकोण क्षेत्र सूत्रों के साथ तालिका
| कच्चा डेटा (कैलकुलेटर पर जाने के लिए सक्रिय लिंक) |
एक स्केच | सूत्र | |
| सभी त्रिकोणों के लिए | |||
| 1 | आधार और ऊंचाई |  |
|
| 2 | दो पक्ष और उनके बीच का कोण |  |
|
| 3 | सर्कल त्रिज्या और तीन तरफ |  |
|
| 4 | परिमित वृत्त और तीन भुजाओं की त्रिज्या |  |
|
| 5 |
तीन पक्ष (हेरॉन के सूत्र के अनुसार) |
 |
जहाँ
|
| 6 | पक्ष और दो आसन्न कोने |  |
|
| Isosceles त्रिकोण के लिए | |||
| 7 | पक्ष और आधार |  |
|
| 8 | उनके बीच के पक्ष और कोण |  |
|
| 9 | भुजाएँ, आधार और कोण पक्षों और आधार के बीच |  |
|
| 10 | आधार और कोण पक्षों के बीच |  |
|
| 11 | ऊंचाई और आधार |  |
|
| समतुल्य त्रिकोण के लिए | |||
| 12 | पार्टी |  |
|
| 13 | ऊंचाई |  |
|
| 14 | वृत्त त्रिज्या |  |
|
| 15 | परिमित वृत्त का त्रिज्या |  |
|
| दाएं कोण वाले त्रिकोणों के लिए | |||
| 16 | दो पैर | 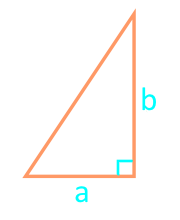 |
|
| 17 | कर्ण और कोण |  |
|
| 18 | पैर और कोने |  |
|
| 19 | जिन खंडों में खुदा हुआ चक्र कर्ण को विभाजित करता है | 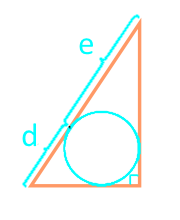 |
|
| 20 | कर्ण और उत्कीर्ण वृत्त त्रिज्या |  |
|
| 21 |
तीन पक्ष (हेरॉन के सूत्र के अनुसार) |
 |
जहाँ
|





