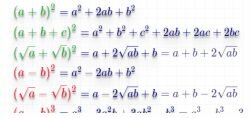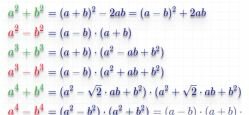Afkorting Formules
Afkorting Formules kunt u een wiskundige uitdrukking omzetten in een eenvoudigere vorm, waardoor u verdere transformaties kunt uitvoeren of de juiste oplossing kunt vinden. Een voorbeeld van formules voor wiskundige transformaties is de ontbinding van polynomen, met behulp waarvan de graad van polynomen wordt verminderd. En met behulp van Newton's Binom wordt bijvoorbeeld decompositie in afzonderlijke termen van de mate van twee variabelen uitgevoerd.
Vereenvoudigingsformules worden gebruikt om haakjes van graden bloot te leggen, de som van een som of een verschil te verminderen, en ook voor andere wiskundige vereenvoudigingen. In onderstaande formules, in plaats van karakters «a» en «b» numerieke waarden, variabelen of wiskundige uitdrukkingen en formules kunnen worden gebruikt.
Onderaan de pagina kunt u formules downloaden in de vorm van afbeeldingen voor later afdrukken en als referentiemateriaal gebruiken bij het oplossen van problemen.
1. Kwadraat bedrag
... ... voorbereiding van formules ... ...2. Verschil vierkant
3. Som en verschil van vierkanten
4. Bedrag in de derde graad
5. Derde graads verschil
6. Som en verschil van kubussen
7. Vierde graads afkorting formules
8. Afkorting Formules van de vijfde graad
9. Zesde graads v afkorting formules
10. Afgekorte vermenigvuldigingsformules voor graden n, waar n - elk natuurlijk getal
11. Afgekorte vermenigvuldigingsformules voor graden n, waar n - zelfs een positief nummer
12. Afgekorte vermenigvuldigingsformules voor graden n, waar n - oneven positief getal
13. Enkele eigenschappen van formules
Download afbeeldingsformules als afbeeldingen
Download afbeeldingsformules
